INTRODUCCIÓN
El análisis de los resultados obtenidos en diferentes evaluaciones internacionales (informes PISA, entre otros) muestra que los conocimientos y niveles de aprendizaje de los alumnos de Educación Obligatoria en Matemáticas son insuficientes. Nos preguntamos ¿Qué hacer para mejorar el aprendizaje y la enseñanza de las matemáticas? La respuesta a esta pregunta la podemos abordar desde diferentes perspectivas. En este trabajo nos vamos a referir a la formación inicial del profesorado como un elemento básico para mejorar y conseguir un aprendizaje de calidad (cognoscitivo, significativo y efectivo) en Matemáticas.
Las propuestas dirigidas a la formación inicial del profesorado de Primaria y Secundaria deben tomar en consideración los resultados de las investigaciones que proporcionan datos sobre las carencias formativas de estos profesores y elaborar propuestas de enseñanza y aprendizaje adecuadas a sus necesidades, de tal manera que se acierte sobre los contenidos disciplinares y las competencias profesionales adecuadas al perfil de los profesores. El análisis de los resultados obtenidos en diferentes evaluaciones internacionales (informes PISA, entre otros) muestra que los conocimientos y niveles de aprendizaje de los alumnos de Educación Obligatoria en Matemáticas son insuficientes. Nos preguntamos ¿Qué hacer para mejorar el aprendizaje y la enseñanza de las matemáticas? La respuesta a esta pregunta la podemos abordar desde diferentes perspectivas. En este trabajo nos vamos a referir a la formación inicial del profesorado como un elemento básico para mejorar y conseguir un aprendizaje de calidad (cognoscitivo, significativo y efectivo) en Matemáticas.
Las propuestas dirigidas a la formación inicial del profesorado de Primaria y Secundaria deben tomar en consideración los resultados de las investigaciones que proporcionan datos sobre las carencias formativas de estos profesores y elaborar propuestas de enseñanza y aprendizaje adecuadas a sus necesidades, de tal manera que se acierte sobre los contenidos disciplinares y las competencias profesionales adecuadas al perfil de los profesores.
Sin embargo, los programas de Matemáticas aplicados con estudiantes para profesores insisten, en general, en un tratamiento de la Matemática desde la perspectiva disciplinar, considerándola como un producto cerrado y acabado. Este enfoque, único, es insuficiente como muestran las investigaciones realizadas. En la formación del profesor de Matemáticas es importante mostrar la relevancia que tiene el carácter específico del dominio de las Matemáticas. Proporcionar a los estudiantes para profesores de Matemáticas, el análisis epistemológico y fenomenológico del conocimiento matemático, objeto de enseñanza de una etapa educativa, supone conocer además de los sistemas conceptuales implicados, sus lenguajes y problemas, la utilidad de los objetos matemáticos y su uso, lo que permitiría abordar con éxito la interpretación de los fines del currículo de matemáticas de esa etapa educativa y afrontar con garantías el conocimiento matemático didáctico.
En este artículo se desarrollan diferentes aspectos relevantes sobre los conocimientos y competencias profesionales de un profesor de Matemáticas, para mostrar ejemplos de buenas prácticas en la formación de los mismos, en relación con el análisis del contenido y el desarrollo curricular que proporciona el dominio de las Matemáticas desde la Competencia Matemática Formal (CMF).
DESARROLLO
1. 22+ 3 × 22 = 2. 3 + √2 = 3. 3 + 3 √2 = 4. 0.3 + 1 /2 + 2 = 5. √5 – 2 = 6. 3x + 3 = 7. 5x + 2 = 8. 4x – 2 + x = 9. 3x + 2y – 3 + y = 10. x + (2x + y) - 2 = |
3) Cuestiones formuladas en formato de problemas, por ejemplo: Los números 1, 4, 9, 16,… reciben el nombre de números cuadrados, ya que pueden ser dispuestos en forma de cuadrados. Se pueden descomponer como sigue: 1=1; 4= 1 + 3; 9= 1 + 3 + 5; 16 = 1 + 3 + 5 + 7
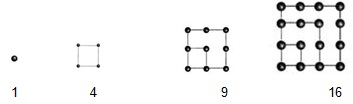
V.1. Calcula el número cuadrado siguiente al 16.
V.2. Calcula el número cuadrado que ocupa la posición 6.
V.3. Calcula el número cuadrado que ocupa la posición 20.
V.4. Calcula el número cuadrado que ocupa la posición n.
En las tareas de un cuestionario o en las que proponemos a nuestros alumnos es necesario realizar el análisis del contenido matemático implícito en cada una de ellas, a efectos de poder estudiar los diferentes significados que los estudiantes muestran en su resolución.
Veamos cómo el Análisis del Contenido que hemos establecido permite determinar los dominios de la actividad matemática en relación con la Competencia Matemática Formal (CMF), es decir, explicitar los objetos del campo conceptual en términos de las operaciones, estructuras y procesos implicados, así como, el contexto en el que se desarrolla la tarea.
En el caso de la tarea 1, se proponen situaciones problemáticas que se sitúan en el conocimiento estructural, que los estudiantes deben identificar y resolver. Esta tarea consta de ocho sentencias que están en registros numéricos y dos en registros algebraicos, que los alumnos deben reconocer y realizar, si es necesario, transformaciones en ellas, y en las que se solicitan, además, justificaciones argumentadas. Los diez ítems están formulados en el ámbito estructural, y se expresa mediante una igualdad en la que las operaciones y las partes deben ser conocidas, se trata de la utilización del signo igual en “sentido lógico”, que inicialmente se pueden identificar con una estructura, un concepto o una propiedad matemática.
La tarea facilita información sobre el comportamiento de los resolutores y cómo actúan frente a cuestiones que implican la identificación de una estructura o una propiedad. Es decir, el dominio de la actividad matemática, permite estudiar el papel de los diferentes registros en las representaciones utilizadas, en términos de si los reconocen, los transforman o elaboran otros apropiados, y el tipo de argumentos que expresan para asegurar la veracidad o no de la sentencia, justificando con fundamentos operacionales basados en operaciones o reglas, o con fundamentos estructurales basados en conceptos, propiedades o estructuras.
En el caso de la tarea 2, se proponen situaciones problemáticas que se sitúan en el conocimiento operacional y que los estudiantes también deben identificar y resolver, en la que cinco de las actividades están formuladas en registros numéricos y las otras cinco están expresadas en registros algebraicos. Se trata de una tarea de diez ítems, formulados mediante sentencias incompletas en las que falta el segundo miembro de la igualdad, y en la que se pide que los alumnos realicen determinados cálculos para obtener el segundo miembro de la misma, de manera que ésta sea verdadera, es decir, sea una identidad. Las diez cuestiones que se plantean, tienen inicialmente un sentido operacional, se trata de la utilización del signo igual en “sentido semántico”, que el alumno identifica como una expresión que debe completar, realizando operaciones, aplicando reglas o técnicas de cálculo adecuadas, es decir, se plantea una igualdad en la que el segundo miembro es desconocido.
Esta segunda tarea facilita información sobre el comportamiento de los resolutores y cómo actúan frente a cuestiones que implican la realización de cálculos para completar una igualdad. Permite analizar las necesidades o no de los estudiantes de dar como resultado una cantidad, aunque sea aproximada, en los apartados numéricos y de observar el tipo de objeto matemático asociado a las expresiones numéricas o algebraicas.
En el caso de la tarea 3, se propone una situación problemática que se sitúa en el conocimiento procesual, en la que de nuevo se pide la identificación y resolución del problema, pero ahora se trata de un proceso de generalización, en el que se da, de forma explícita, una descripción organizada de un comportamiento regular, en dos representaciones diferentes, en el que la regla no viene dada de forma explícita. Se trata de establecer una igualdad, en la que alguna operación o alguna parte son desconocidas y están por determinar.
Se sitúa la tarea en el desarrollo de las competencias generales de todo proceso matemático: reconocerlo, formularlo y manipularlo, que en este caso, se concretan en los cuatro momentos que caracterizan el proceso de generalización.
La tarea se organiza, en diferentes apartados, en la que se pide determinar otros números cuadrados más o menos cercanos a los que se facilitan, en uno de los dos registros, para terminar expresando el número cuadrado en la posición “n”.
CONCLUSIONES
La formación del profesorado de Matemáticas debe orientarse a la organización y desarrollo de buenas prácticas que permitan la consecución de las competencias profesionales requeridas; estas se tienen que desarrollar en el marco de la resolución de problemas de carácter profesional relacionados con los conocimientos y recursos que el profesor debe movilizar para obtener la solución del problema profesional requerido, en esta caso hemos analizado: “Organizar el contenido matemático para enseñarlo”.
En la organización del contenido matemático para enseñarlo, encontramos que el punto de partida es la organización del contenido matemático desde el punto de vista disciplinar. En este sentido, se ha propuesto una organización de la Matemática como disciplina multiforme, en la que se destacan tres aspectos como esenciales:La Matemática es un LENGUAJE simbólico característico y constituye un sistema de signos propios; La Matemática es un SISTEMA CONCEPTUAL lógicamente organizado y socialmente compartido; La Matemática es una actividad de RESOLUCIÓN DE PROBLEMAS socialmente compartida. El campo conceptual es organizado mediante los referentes: Operaciones, Estructuras y Procesos, que permite establecer los dominios de la actividad matemática que tiene lugar en un contexto concreto, caracterizado por la Situación Problemática (Plantear y resolver problemas), el Lenguaje (Comunicar) y los Razonamientos (Pensar y Argumentar), que son también elementos socioculturales comunes a cualquier disciplina curricular y en consecuencia organiza también las restantes competencias asociadas a la especificidad de la propia disciplina Matemática.
Esta forma de organizar la Competencia Matemática Formal (CMF) permite describir el campo conceptual del objeto, sus funciones y su fenomenología, en el nivel temático en que estemos tratando el objeto matemático.
La CMF es un instrumento útil que posibilita también relacionar y describir, tomando en consideración el contexto, los significados de los objetos matemáticos y sus relaciones, tanto a nivel individual como institucional, los errores, las dificultades y los obstáculos.
Este trabajo ha sido financiado por el Plan Nacional de Investigación del Ministerio de Ciencia e Innovación mediante el Proyecto: "Modelos de competencia formal y cognitiva en pensamiento numérico y algebraico de alumnos de Primaria, de Secundaria y de Profesorado de Primaria en formación". (EDU2011-29324).
REFERENCIAS BIBLIOGRÁFICAS
Ball, D., Thames, M. H. & Phelps, G. (2008). Content knowledge for teaching: what makes it special? Journal of TeacherEducation, 59(5), 389-407.
BOC (2007). DECRETO 127/2007, de 24 de mayo, por el que se establece la ordenación y el currículo de la Educación Secundaria Obligatoria en la Comunidad Autónoma de Canarias. (Boletín Oficial de Canarias núm. 113, jueves 7 de junio de 2007).
Hernández, J.; Muñoz, M. Palarea, M.M.; Ruano, R. y Socas, M.M. (2010). La programación por competencias en la clase de Matemáticas. Una actividad profesional básica. En M.T. González, M.M. Palarea y A. Maz, (Eds.), Seminario de los grupos de investigación pensamiento numérico y algebraico e historia de la educación matemática (pp. 26-49). Salamanca: SEIEM.
Rico, L. y Lupiáñez, J. L. (2008). Competencias matemáticas desde una perspectiva curricular. Madrid: Alianza Editorial.
Shulman, L. (1986). Those who understand: Knowledge growth in teaching. EducationalResearcher, 15(2), 4-14.
Socas, M. M. (2010). Competencia matemática formal. Un ejemplo: el Álgebra escolar. Formación del Profesorado e Investigación en Educación Matemática X, pp. 9-43.
Socas, M. M. (2011). Aprendizaje y enseñanza de las Matemáticas en Educación Primaria. Buenas prácticas. Educatio Siglo XXI, Vol. 29 (2), pp. 199-224. ISSN: 1699-2105.
Socas, M. M. (2012). El análisis del contenido matemático en el enfoque lógico semiótico (ELOS). Aplicaciones a la investigación y al desarrollo curricular. En Arnau, D., Lupiáñez, J. L. y Maz, A. (Eds), Investigaciones en Pensamiento Numérico y Algebraico e Historia de la Matemática y Educación Matemática (pp. 1-22). Valencia: Departamento de Didáctica de la Matemática de Universitat de Valencia y SEIEM.
Socas, M. M., Hernández, J., Palarea, M. M., Afonso, M. C. (2009). La influencia del pensamiento operacional en el aprendizaje de las Matemáticas y el desarrollo de las competencias matemáticas Indivisa. Boletín de Estudios e Investigación. Monografía XII, 101-119.