INTRODUCCIÓN
La enseñanza de la física, en cualquier nivel educativo no es una tarea fácil, sobre todo si se considera que la mayoría de los estudiantes tienen la creencia de que esta es una asignatura difícil de entender y cuyo lenguaje, las matemáticas, la hace mucho más incomprensible y confusa. Paradójicamente, al mismo tiempo se aprecia que en los últimos años los medios de comunicación han implementado y modernizado secciones dedicadas a la divulgación de temas científicos, de forma que los estudiantes tienen fácil acceso a la información, sobre todo a través de la Internet, haciendo que algunos temas de física que en principio pudieran parecer especializados se conviertan en parte de su cultura general.
Actualmente, el docente se encuentra ante el reto de lograr que los estudiantes, además de aprender física de forma significativa, se diviertan, se motiven y la dejen de ver como algo alejado de su vida cotidiana. Una propuesta sería presentarla como un área científica del conocimiento en continuo desarrollo, en donde las ideas evolucionan y muchas veces se consolidan en la generación de la nueva tecnología que cotidianamente se utiliza para hacer más sencilla y cómoda nuestra vida.
Dentro de la gran diversidad de temas que se presentan en los programas de estudio de las asignaturas de física, destaca el relacionado con la interacción electromagnética pues esta, a diferencia de las otras tres interacciones fundamentales, se encuentra presente, de forma preponderante, en toda escala, desde lo macroscópico hasta lo microscópico. La interacción electromagnética determina la estructura atómica, pues los electrones se mantienen unidos al núcleo debido a ella, mientras que la fuerza gravitacional que existe entre estas partículas es 40 veces más pequeña por lo que no es significativa.
A su vez, la fuerza ejercida entre dos átomos próximos es precisamente la fuerza electromagnética entre sus electrones y núcleos. Las fuerzas que se analizan en otros ámbitos de la física como son la fricción, la tensión superficial, el empuje, etc., son en realidad el resultado de esta interacción electromagnética. Lo anterior permite afirmar que todas las fuerzas que se observan en nuestra vida cotidiana, con excepción de la gravedad, son de origen electromagnético e inclusive cabe recordar que nuestro cuerpo funciona debido a impulsos eléctricos.
Por otra parte, los conceptos básicos del electromagnetismo no solo explican gran parte de los fenómenos que gobiernan la física y la química de la materia ordinaria sino que además tienen una gran importancia práctica puesto que nuestra civilización está basada en la producción de energía eléctrica y su aplicación en motores, generadores, alumbrado, calefacción, aparatos médicos, etc. .Además, es importante recordar que desde un punto de vista más específico, la estructura teórica del electromagnetismo ha permeado a otras áreas de la física y del conocimiento científico.
De esta manera, nuestra forma de vida y nuestra vida diaria no sería como la conocemos si no hubiese un estudio sistemático del electromagnetismo y sus aplicaciones.
La enseñanza de los conceptos básicos de la física se encuentra obligatoriamente en los programas de estudio que se aplican desde el nivel escolar básico hasta el nivel medio superior y en estos siempre se incluye la discusión de algunos de los conceptos básicos del electromagnetismo ya que resultan indispensables en la formación integral de todo estudiante, independientemente de si elegirá o no a la física, u otra carrera afín, como el campo en el que se desarrollará profesionalmente. Puesto que prácticamente toda la tecnología que se encuentra a nuestro alcance está basada en algún concepto de electromagnetismo, un conocimiento básico de este introducirá al estudiante al pensamiento científico y le proporcionará un mejor entendimiento del entorno que le rodea.
DESARROLLO
LA ENSEÑANZA DEL ELECTROMAGNETISMO EN EL NIVEL SUPERIOR
En el nivel superior, en la licenciatura en física, en química y en algunas de las ingenierías, el electromagnetismo se convierte en una asignatura obligatoria y usualmente se imparten al menos dos cursos, uno a nivel básico y otro sobre temas avanzados, en los que los conceptos básicos se discuten en mayor o menor detalle dependiendo del perfil de egreso. En general, independientemente de la licenciatura, estos cursos presentan un alto índice de reprobación convirtiéndolos en un problema para la eficiencia terminal de la licenciatura. Probablemente, los mayores obstáculos con los que se encuentran los estudiantes en estos cursos sean el manejo de las herramientas matemáticas, la abstracción y la complejidad de los conceptos que se discuten.
Un caso particular es el de la Licenciatura en Física que se imparte en la Facultad de Ciencias de la Universidad Nacional Autónoma de México y cuya duración es de nueve semestres. En esta licenciatura, los estudiantes deben cursar dos asignaturas obligatorias: “Electromagnetismo I”, en el cuarto semestre, y “Electromagnetismo II”, en el séptimo semestre. Aunque ambos cursos presentan un alto índice de reprobación, el caso de Electromagnetismo I resulta más preocupante por tratarse de una asignatura de formación básica en la que los problemas en el aprendizaje generan en el estudiante un sentimiento de frustración que en muchas ocasiones lo desalienta y lo lleva a abandonar el curso.
En los semestres impares, en los cuales los alumnos que usualmente se inscriben son alumnos que previamente habían reprobado la asignatura o que van desfasados con respecto a su generación, el índice de aprobación en la mayoría de los casos apenas sobrepasa el 40%, mientras que en los semestres pares en donde la gran mayoría de los estudiantes es la primera vez que cursan la asignatura, el índice de aprobación es del 50%. Estas cifras indican que existe un serio problema, en el que se debe revisar cada una de las posibles facetas para determinar las razones que llevan al fracaso escolar. En este trabajo se analizan los problemas que enfrentan los estudiantes cuando intentan aplicar las herramientas matemáticas en el estudio de los conceptos básicos de electromagnetismo.
Aunque todo estudiante de la asignatura básica de electromagnetismo ha cursado por lo menos dos cursos básicos de cálculo diferencial e integral y geometría analítica, y un curso básico de álgebra, álgebra lineal, y ecuaciones diferenciales, el lenguaje, el tipo de conocimientos y problemas que se resuelven en estos cursos de matemáticas están más enfocados a la parte abstracta del concepto que a su aplicación a la solución de los problemas de la física. Muchas veces, cuando el conocimiento es abstracto y tiene consecuencias cotidianas que son familiares a los estudiantes, estos tienden a utilizar su sentido común en una manera que les conduce a cometer errores conceptuales. Es usual que en un curso de electromagnetismo el profesor se incline por impartir una clase magistral en la que se expone el tema sin más ayuda que el gis y el pizarrón para posteriormente resolver una gran cantidad de ejercicios que usualmente son los ejemplos resueltos de los libros de texto, o pequeñas variaciones a estos.
En clase, el estudiante cree comprender el concepto y se siente seguro de poder aplicarlo en la resolución de problemas. Al estudiar para el examen se enfoca solamente en la información que presenta el libro de texto y sus notas de clase y vuelve a repasar los ejemplos resueltos. Sin embargo, cuando trata de resolver los problemas de final de capítulo o los problemas de examen se da cuenta de que tiene serias deficiencias conceptuales y que muchos de ellos tienen que ver con su poca habilidad para aplicar las herramientas que ya ha adquirido en sus cursos de matemáticas. Dicho así, uno de los retos en la labor docente del profesor es el diseño de nuevos problemas o retos en los que el estudiante pueda entender claramente la forma en la que los conceptos se aplican. A continuación se enuncian los temas básicos que constituyen un programa del curso de electromagnetismo y los problemas más comunes que los estudiantes presentan. Debemos recalcar que el tipo de dificultades que el estudiante encuentra son diferentes cuando no conoce la explicación física o no puede construir modelos que le lleven a ella con las dificultades inherentes solo al manejo de la herramienta matemática.
La ley de Coulomb
Es común, que la enseñanza del electromagnetismo tome como punto de partida la electrostática tomando como puntos básicos el concepto de carga y la interacción entre estas, expresada a través de la Ley de Coulomb.
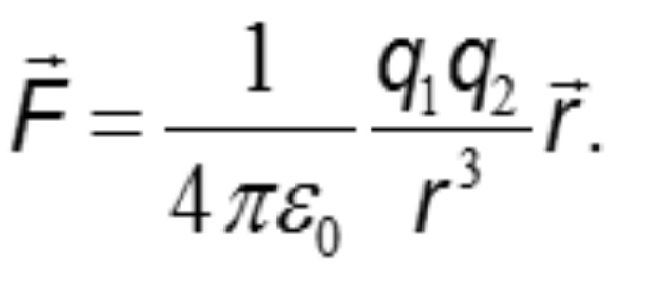
Pese a que este tema ha sido estudiado en el nivel medio superior e incluso se menciona en los cursos de educación básica, la mayoría de los estudiantes encuentra en él un primer obstáculo en el estudio del electromagnetismo. En los cursos de física de los niveles educativos anteriores este tema se analiza de manera cualitativa y se resuelven problemas en una dimensión, lo que contribuye a la confusión del estudiante cuando se trata de resolver problemas en tres dimensiones (Ngoc-Loan, 2003) y en donde el profesor calcula la fuerza que experimenta una carga debido a un sistema de cargas colocadas en posiciones arbitrarias.
Cabe mencionar que en los cursos de Mecánica Clásica, que siempre se consideran como un requisito para inscribir el curso de electromagnetismo, el estudiante ha trabajado con el concepto de fuerza como un vector aplicándolo a la solución de una gran cantidad de problemas. En un intento por aplicar la transferencia del conocimiento, el profesor discute la gran similitud entre la Ley General de Gravitación de Newton y la expresión para la fuerza de Coulomb con la esperanza de que el estudiante reconozca la generalidad de la física y pueda plantear y resolver los problemas.
Cabe resaltar que el álgebra vectorial ha sido estudiada con todo detalle en los cursos de matemáticas correspondientes y resulta interesante hacer notar que en esos cursos algunos estudiantes pueden sumar con gran facilidad vectores, sin embargo, cuando se les pide hacer lo mismo, pero ahora inmersos en un contexto físico, tienen dificultades para hacerlo correctamente, lo que es un problema común como exhibe Planinic (2006).
A pesar del esfuerzo del profesor, al estudiante se le dificulta calcular la fuerza que ejercen entre sí partículas cargadas principalmente por el hecho de que ahora la fuerza puede ser tanto atractiva como negativa dependiendo del signo de las cargas. El problema se complica aún más cuando se trata con sistemas constituidos por más de dos cargas en los que se tiene que aplicar el principio de superposición y por ende se deben sumar vectores.
Aunque los estudiantes dibujan correctamente un diagrama de cuerpo libre, es común que se equivoquen en la suma de vectores al tratarlos como escalares simplemente sumando las magnitudes de los vectores. En este punto es necesario repasar cuáles son las principales características de un vector y las operaciones básicas con esta entidad matemática.
Otro error común se tiene cuando los estudiantes se confunden al definir su sistema de referencia y expresar a la fuerza en términos de sus componentes.
En casos extremos algunos estudiantes llegan incluso a tratar de dividir vectores.
El concepto de campo eléctrico
Uno de los conceptos más importantes en la física es el de campo y en el caso del electromagnetismo el estudiante debe enfrentarse al reto de asimilar el concepto de campo eléctrico y, posteriormente, el de campo magnético, ambos conceptos abstractos y que no pueden asociar tan fácilmente a su realidad como el caso del campo gravitacional, que, desde luego, está directamente asociado con el tiro parabólico y lo que conocen del movimiento planetario. Un aprendizaje significativo de conceptos científicos claves, como el concepto de campo, es una condición necesaria para la formación científica de los estudiantes, su comprensión de los fenómenos físicos y el conocimiento de principios que sustentan diversas aplicaciones tecnológicas.
El campo eléctrico en un punto del espacio se define en términos de la fuerza por unidad de carga que experimentaría una partícula cargada de prueba al colocarse en ese punto, por lo que los mismos problemas con el manejo de vectores que enfrenta el estudiante en el cálculo de la fuerza de Coulomb vuelven a aparecer. Ahora, además de comprender el concepto de campo deberá entender la figura matemática de campo vectorial, es decir, una función que asocia a cada punto del espacio un vector que posee una magnitud y una dirección.
El cálculo del campo generado por una distribución de carga.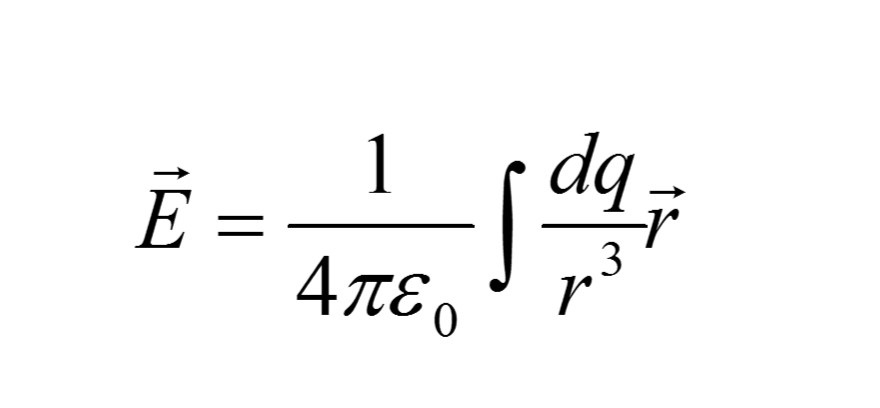
La Ley de Gauss
En la ley de Gauss se manifiesta de forma explícita el modelo de campo en vez de un modelo de acción a distancia y en los casos en los que la distribución de carga tiene una simetría bien definida nos permite calcular el campo eléctrico. En la solución de problemas con la expresión integral de la ley se Gauss,
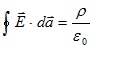
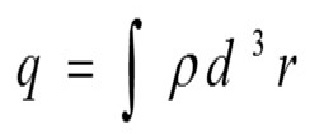
Dependiendo de la simetría de la distribución de carga, debe elegirse la superficie gaussiana que facilite el cálculo de la integral de superficie y utilizar el sistema de coordenadas adecuado. Los estudiantes están acostumbrados a trabajar en coordenadas cartesianas e integrar en estas coordenadas, pero tienden a confundirse cuando deben utilizar coordenadas esféricas y, sobre todo, coordenadas cilíndricas.
Una vez establecida la simetría del problema también les resulta difícil plantear las integrales involucradas, problema que se ve acrecentado cuando se plantean ejercicios que involucran distribuciones de carga no homogéneas, lo que lleva necesariamente a tener que calcular integrales sobre volúmenes para calcular la carga encerrada por la superficie gaussiana.
En algunos casos los estudiantes, tomando como ejemplo los ejercicios resueltos en los libros de texto usuales (Alonso, 1995; Ohanian, 2009; Resnick, 1996; Sears, 1999; Serway 2004),consideran al campo eléctrico como una constante que puede sacarse del signo de integral, lo que en algunos casos es incorrecto.
Ahora bien, para llegar a la forma diferencial de la Ley de Gauss,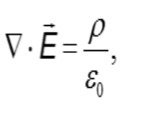
Potencial Eléctrico
Los alumnos no tienen una clara idea del concepto de potencial eléctrico, y tienen dificultades para distinguir y utilizar términos como diferencia de potencial, energía potencial eléctrica, voltaje, corriente, energía, potencia, etc. Los términos corriente eléctrica, electricidad y voltaje los utilizan como sinónimos. Esta confusión puede deberse a que el concepto de potencial eléctrico se relaciona cotidianamente con el concepto de corriente eléctrica. En el cálculo de la diferencia de potencial entre dos puntos del espacio como el trabajo por unidad de carga que debe realizar un agente externo para llevar a una partícula cargada de prueba de un punto a otro, el estudiante deberá calcular la integral
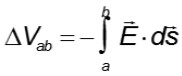
tomando en cuenta que es independiente de la trayectoria que se elija entre el punto a y el punto b. En este tema, uno de los problemas usuales que se encuentra el estudiante es el cálculo de esta integral de línea.
Otro de los problemas se presenta cuando queremos encontrar el campo eléctrico como menos el gradiente del potencial eléctrico, lo cual significa que se deberán calcular derivadas parciales del potencial eléctrico con respecto a cada una de las componentes.
Fuerza que experimenta una partícula cargada en un campo magnético
En el cálculo de la expresión
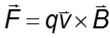
el producto vectorial representa un problema ya que es claro que ahora deberán trabajar con vectores y el resultado del producto cruz es un vector. La mayoría de los estudiantes encuentra difícil definir la dirección en la cual apunta la fuerza, lo cual indica una baja asimilación del concepto de producto vectorial o producto cruz.
Ley de Biot-Savart
La ley de Biot-Savart que nos permite calcular el campo magnético generado por una distribución de corriente resulta complicada de aplicar no solo por los problemas ya mencionados en relación con el manejo de vectores, sino que ahora se le tiene que agregar que el argumento de la integral contiene un producto vectorial, ya que
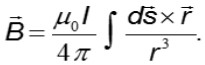
Ley de Ampère
En este caso, no solamente se vuelven a presentar las dificultades mencionadas con la ley de Gauss (Guisasola, 2003, 2008; Wallace, 2010) sino que ahora los conceptos involucrados de integral de línea cerrada y orientación de una superficie abierta contribuyen a aumentar las dificultades de los alumnos. La integración que se tiene que hacer es:
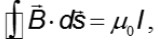
donde
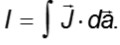
es la corriente que atraviesa la superficie abierta encerrada por el contorno cerrado. También es necesario tomar en cuenta que para calcular el campo magnético por este método se debe de tener la simetría apropiada lo cual implica no solo escoger el contorno cerrado apropiado con las coordenadas correspondientes, sino también usar la regla de la mano derecha para saber la dirección del campo magnético una vez que se conoce la dirección de la corriente eléctrica. Más aún, en caso de densidades de corriente no homogéneas los estudiantes se encuentran con el problema de calcular la corriente que atraviesa el circuito amperiano.
Entonces llegar a la expresión diferencial de la Ley de Ampère implica aplicar el Teorema de Stokes y en la resolución de problemas aplicar el operador rotacional, el cual implica derivadas parciales y al producto vectorial.
Ley de Faraday
Aquí vuelven a aparecer los problemas mencionados en relación a la ley de Ampère, además de que ahora el estudiante debe determinar el sentido de la corriente inducida, la cual tiene que concordar con la Ley de Lenz.
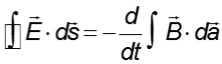
Se debe enfatizar en el hecho de que los alumnos procuren recordar que es necesario derivar el flujo de campo magnético, ya sea para determinar el sentido de la corriente inducida o para calcular el campo eléctrico inducido.
Ondas electromagnéticas
Cotidianamente el estudiante ha escuchado hablar de las ondas electromagnéticas, este concepto se encuentra en la tecnología que le es familiar, por ejemplo en el horno de microondas o en el teléfono celular que se ha convertido en uno de sus dispositivos electrónicos indispensables. Cuando se obtiene la ecuación de onda a partir de las ecuaciones de Maxwell, deben aplicarse las operaciones comunes entre los vectores y los operadores vectoriales. Por otra parte, deberá resolverse una ecuación diferencial de segundo grado homogénea. En la radiación electromagnética está involucrado el concepto de campo eléctrico y campo magnético como vectores. Así pues, es común que se presenten los mismos problemas en la aplicación de las herramientas matemáticas que hemos mencionado.
CONCLUSIONES
Desde un inicio, las matemáticas y la física han constituido un binomio inseparable, pues no podemos concebir a una sin la otra. El desarrollo de las matemáticas se ha visto fortalecido por el avance de la física y nuevas teorías matemáticas surgen junto con teorías de la física. Por otro lado, para la física las matemáticas constituyen un lenguaje que le permiten describir, modelar y predecir lo que ocurre en la naturaleza. Así que es imposible diseñar un curso de física en el nivel superior en el que las matemáticas no se encuentren presentes. En particular, los cursos de electromagnetismo requieren que el estudiante tenga un conocimiento básico de las herramientas matemáticas de forma que estas no se conviertan en un obstáculo para el aprendizaje.
Aunque en la licenciatura en física los estudiantes inscritos en la primera asignatura de electromagnetismo deben haber tomado los cursos básicos de cálculo diferencial e integral, en los que además se incluye al cálculo vectorial, presentan serios problemas en la resolución de problemas dado que en sus cursos de matemáticas los conceptos básicos les fueron enseñados de forma totalmente abstracta sin plantear la estrecha relación entre las matemáticas y la física, dificultando con ello la enseñanza de los conceptos básicos del electromagnetismo.
Con el objetivo de mejorar la enseñanza en los cursos del electromagnetismo en el nivel superior, el docente deberá aplicar una estrategia didáctica en la cual se contemplen los siguientes puntos:
La aplicación de cuestionarios de evaluación que permitan determinar el nivel de conocimiento, el manejo y la comprensión de las herramientas matemáticas necesarias.
La aplicación de cuestionarios cuyo objetivo sea determinar las ideas previas de los estudiantes sobre algunos conceptos básicos del electromagnetismo que son de uso cotidiano, como por ejemplo carga, potencial eléctrico, corriente eléctrica, etc.
Motivar al estudiante al estudio del electromagnetismo mediante la actualización continua de la información y la discusión de las aplicaciones del electromagnetismo de forma que sienta cercanos a él los conocimientos que está adquiriendo.
Mostrar al estudiante la importancia del electromagnetismo como generador de nuevas teorías en la física y nueva tecnología. Generar recursos y material didáctico, como la presentación de experimentos demostrativos, simulaciones y recursos multimedia, que favorezcan el aprendizaje, considerando que para que se produzca un aprendizaje significativo es necesario que el material posea un significado en sí mismo y debe estar constituido por elementos que se relacionen entre sí.
Hacer uso de las TIC de manera que el uso de ejemplos visuales favorezca el aprendizaje sobre todo de los conceptos que requieran de un mayor nivel de abstracción (Alvarez, 2010).
Fomentar la participación del estudiante en la construcción del conocimiento a través del desarrollo de proyectos experimentales.
La resolución de problemas diferentes a los presentados en los libros usuales de electromagnetismo
La evaluación del proceso de aprendizaje.
REFERENCIAS BIBLIOGRÁFICAS
Álvarez, T. (2010). La visualización de conceptos matemáticos y el aprendizaje del electromagnetismo. Latinoamerican Journal of Physics Education, 4, 143-148.
Alonso, M. y Finn, E. J. (1995).Física. Vol. II: Campos y ondas. México: AddisonWesley Iberoamericana.
Guisasola, J., Almundi, J. M., Salinas, J., Zuza, K. & Ceberio, M. (2008). The Gauss and Ampère Laws: different laws but similar difficulties for student learning. European Journal of Physics, 29, 1005.
Guisasola, A. J., Salinas, J., Almudi, J., y Velazco, S. (2003). Análisis de los procesos de aplicación de las Leyes de Gauss y Ampère por estudiantes universitarios de España y Argentina. Revista Brasileira de Ensino de Física l, 25, 195-206.
Ohanian, H. C.& Markert, J. T. (2009).Física para Ingeniería y Ciencias, Vol. 2, 3a. Edición.México: Mc-Graw Hill.
Ngoc-Loan. N. & Meltzer, D. E. (2003).Initial understanding of vector concepts among students in introductory physics courses. American Journal of Physics, 71, 630.
Planinic, M. (2006). .Assessment of difficulties of some conceptual areas from electricity and magnetism using the Conceptual Survey of Electricity and Magnetism. American Journal of Physics, 74, 1143-1148.
Resnick R., Halliday, D., Krane, S.K. (1996). Física, Vol. II, 5a. edición. México: Compañía Editorial Continental.
Sears F. W., Zemansky M. W., Young H. D.& Freedman R. A. (1999).Física Universitaria, Vol. 2, novena edición. México: Pearson Education.
Serway, R. A. y Jewett, J. W. (2004).Física II, 3a. Edición. México: Thomson Learning.
Wallace, C. S. & Chasteen, S. V. (2010). Upper-division students’ difficulties with Ampère’s law. Physical Review Special Topics-Physics Education Research, 6, 20115.