INTRODUCCIÓN
En un mundo caracterizado por un vertiginoso desarrollo de la ciencia y la tecnología y su influencia directa en la producción y la sociedad en general, la formación científica de ciudadanos, constituye hoy, uno de los principales pilares para lograr una cultura general e integral, en todos los sectores de la población cubana. Los cambios ocurridos en la ciencia y el nuevo papel que comienza a asumir esta, apuntan hacia la necesidad de realizar profundas transformaciones en su enseñanza, en particular de la física.
La ciencia estudia todos los fenómenos de la realidad, por tanto, existen ciencias particulares que estudian un sistema cualitativamente determinado de leyes que actúan en el mundo, a saber, mecánicas, físicas, biológicas y económicas, entre otras. Sin embargo, en la actualidad se trabaja en equipos multidisciplinarios, tratando de resolver problemas que involucran a varias especialidades. Lo anterior tiene su reflejo en la enseñanza, que se encuentra en profundas transformaciones. Por tanto, lograr la interdisciplinariedad se convierte en un reto y constituye uno de los principios rectores para el diseño y desarrollo de los currículos en las universidades con el objetivo de formar al profesional de la educación que la sociedad necesita.
Teniendo en cuenta la experiencia histórica y las nuevas condiciones de la educación en Cuba, el Ministerio de Educación ha decidido la elaboración y puesta en práctica de los planes de estudio D. En ellos, se expresa la aspiración de formar un profesional revolucionario con una preparación político – ideológica y científico - metodológica, que le permita dirigir el proceso educativo y en particular, el proceso de enseñanza - aprendizaje de la Matemática y de la Física en los diferentes tipos de instituciones de las enseñanzas Secundaria Básica, Preuniversitaria, Técnica y Profesional y de Adultos y, para aquellos que reúnan los requisitos y preparación necesarios, la docencia universitaria. Este aprendizaje debe realizarse con un enfoque interdisciplinario en que se articulen las relaciones entre la ciencia, la tecnología, la sociedad y el medio ambiente en las condiciones de la Revolución Cubana.
En Cuba, en el proceso de enseñanza - aprendizaje de las asignaturas que conforman el currículo de la carrera para los estudiantes que se forman como profesores con el doble perfil - matemático y físico -, se precisa de la integración de los sistemas de conocimientos de estas asignaturas, así como de métodos y procedimientos que faciliten la comprensión de conceptos, leyes, proposiciones y especialmente al proceso de resolución de problemas, que conducen a la búsqueda y obtención de nuevos conocimientos evitando así, la fragmentación de estos contenidos y la formación de dos modos de actuación diferentes.
En tal sentido, en este artículo se plantea como objetivo contextualizar el programa heurístico general a la resolución de problemas de Física, los cuales requieren del contenido de la disciplina Análisis Matemático. Se presentan dos ejemplos extraídos del curso de Física General I que se desarrolla en el segundo año de la Carrera Matemática Física.
DESARROLLO
Sin un proceso interdisciplinario pertinente no puede existir una educación científica de excelencia, ello se sustenta en las siguientes ideas: La interdisciplinariedad es necesaria para la formación profesional, entre otras razones, porque la actividad profesional en el mundo actual involucra la participación de un equipo de especialistas que se desenvuelven en un clima de respeto mutuo, de igualdad y flexibilidad como premisas para la solución conjunta de los problemas y el desarrollo de las tareas investigativas. (Perera, F., 2000.)
Cuando el hombre aprende a ver la interconexión de la ciencia y la sociedad le es más fácil comprender y apreciar los hechos y fenómenos de la realidad. Con mayor seguridad asume responsabilidad por todo lo que ocurre en el mundo, sin lo cual, propiamente dicho, no hay ni puede haber un auténtico científico y ciudadano. (Ershov, Y., 1987)
“Esta educación científica del individuo ha de conducirlo no sólo a saber de ciencia, sino también sobre la ciencia: sus aspectos culturales, epistemológicos, éticos, sus relaciones con la tecnología y su repercusión social” (Nuñez, J., 1998). En correspondencia con lo anterior: Formar profesores de Matemática - Física que sean capaces de aplicar los conceptos no solo en las situaciones tradicionales de la Matemática sino también y especialmente en las situaciones propias de la Física, asimilando un modelo de actuación acorde con lo que se espera que puedan hacer en su desarrollo profesional posterior (Contreras. 2014, p. 15),es una necesidad impostergable. Entonces, si se quiere formar un profesor capaz de impartir la Física explotando sus relaciones con la Matemática, ¿cómo enseñarle la Matemática con un enfoque que no sea interdisciplinario? Los modelos de actuación de los profesores en el pregrado tienen que estar en correspondencia con los modelos de actuación que se exigen para la vida profesional del futuro egresado. (Contreras. 2014, p. 15)
Los estudiantes de la carrera de Licenciatura en Educación, especialidad Matemática-Física deben egresar con una preparación para impartir las dos asignaturas por igual, entonces ¿cómo es posible que cumplan con la exigencia de impartir las dos disciplinas si en su propia formación no reciben estas con el grado de integración suficiente? De acuerdo con lo anterior, la enseñanza de los conceptos matemáticos en el nivel superior debe relacionarse estrechamente con la Física y en lo posible con los contenidos de ambas disciplinas que se dan en la escuela media.
La enseñanza de las asignaturas de la disciplina Física General necesitan de los contenidos de la disciplina Análisis Matemático, aunque en ocasiones al estudiante no se le explicita la importancia que tienen para comprender la física; esto sucede fundamentalmente porque no siempre existe coherencia en el lenguaje que a veces difiere de una asignatura a otra lo que es resultado de la tradición en la enseñanza de ambas ciencias por separado.
Si se parte de la definición de conceptos físicos y se asume que las magnitudes físicas - que pueden ser escalares o vectoriales - son funciones matemáticas porque se relacionan entre sí, expresando leyes y que además los problemas físicos se resuelven aplicando los conceptos y leyes, por lo que es posible encontrar nodos cognitivos principales en la disciplina Análisis Matemático que permitan el establecimiento de relaciones interdisciplinarias que pueden ser utilizadas consecuentemente en la resolución de problemas de Física que aparecen en determinados libros de problemas con un nivel superior.
En la fundamentación de los programas de las disciplinas Análisis Matemático y Física General, se expresa la necesidad de establecer relaciones interdisciplinarias; pero no se explicita cómo hacerlo, aunque se reconoce que la matemática está presente en la conformación de los conocimientos físicos y a su vez que al ser la matemática el lenguaje de la física, es portadora de un estricto sentido físico.
Por su parte en las indicaciones metodológicas y de organización del Plan D de la carrera Matemática - Física vigentes desde el curso 2010-11 se plantea que:
La disciplina Análisis Matemático está indisolublemente ligada a los contenidos matemáticos que se desarrollan en la escuela, al conducir por una parte del estudio de las propiedades globales de las funciones a la investigación de sus propiedades locales, y por otra, ampliar su dominio de definición a regiones de R2, sobre la base de la apropiación y aplicación de conceptos y métodos del cálculo infinitesimal, en particular, los referidos al límite, la continuidad, la derivación y la integración de funciones de una y dos variables reales. Generaliza además el estudio de las ecuaciones al examen de las ecuaciones diferenciales ordinarias y muestra la potencia de los métodos numéricos en la actualidad para la resolución aproximada de diversos problemas de aplicación. Los contenidos de esta disciplina permiten realizar cálculos aproximados, interpretar y modelar situaciones problemáticas, entre otros interesantes problemas, que son también de extraordinaria importancia para otras ciencias, y en particular, para la física. (MINED. 2010, p.7) De igual manera en este documento se plantea que:
La disciplina Física General aborda los descubrimientos y leyes esenciales que en el desarrollo histórico de la física la han convertido en una de las ciencias naturales trascendentes para la comprensión por el hombre del mundo que le rodea y para su transformación en beneficio o perjuicio de la naturaleza y la sociedad, lo cual es de vital importancia para la formación del futuro profesor de Matemática y Física. Particular atención se le prestan a los núcleos de contenidos en los temas relacionados con la cinemática, la dinámica, la teoría cinético-molecular, la termodinámica, el electromagnetismo, las oscilaciones y ondas, la óptica geométrica, la teoría especial de la relatividad, la física del átomo y del núcleo, la cosmología y la física de las partículas elementales. (MINED. 2010, p.7)
Según el plan de estudio de la carrera Licenciatura en Educación en Matemática - Física, la disciplina Física General está constituida por seis asignaturas, la primera de ellas Física General I: Mecánica, se imparte en el primer semestre de segundo año. Esta tiene como objeto de estudio el movimiento mecánico, uno de los cambios más importantes que se operan en los sistemas físicos y que constituye interés primario en el objeto de estudio de la disciplina Física General. Los conceptos y leyes que se abordan en la asignatura constituyen la base de los contenidos del resto de las asignaturas de la disciplina y es por esa razón que la Mecánica ocupa la primacía entre todas.
Esta asignatura tiene como contenidos esenciales: El estudio de la Física como ciencia y como asignatura. Mediciones. Vectores. Movimiento mecánico unidimensional, bidimensional y tridimensional. Fuerza y las leyes de Newton. Interacciones fundamentales en la Naturaleza. Dinámica de la partícula. Trabajo y energía. Conservación de la energía. Sistema de partículas. Colisiones. Cinemática y Dinámica de la rotación. Leyes de conservación de la energía mecánica, del momento lineal, del momento angular y de la paridad. Oscilaciones. Gravitación. Ley de gravitación universal. Estática y dinámica de los fluidos. Movimiento ondulatorio. Teoría especial de la relatividad y elementos de la teoría general.
A partir de lo anterior resulta importante tener en cuenta en la enseñanza de la Física General los contenidos del Análisis Matemático para lograr impartir un curso con un nivel mayor de profundidad en sus contenidos físicos, a la vez que se logra sistematizar los contenidos del Análisis Matemático. En el proceso de enseñanza - aprendizaje de la asignatura Física hay tres actividades típicas, a saber, tratamiento de los conocimientos teóricos, las prácticas de laboratorio y la resolución de problemas. En este artículo se ha centrado la atención en la resolución de problemas físicos docente que requiera el empleo de los contenidos del Análisis Matemático.
La resolución de problemas se trata en la enseñanza de las ciencias a través de diversas tareas, que están presentes en la enseñanza de la Física, pero estas tareas en muchas ocasiones tienen varios puntos de contacto mediante relaciones interdisciplinarias que en la actualidad se manifiestan en la enseñanza de la Matemática, la Física y las ciencias en general. (Pino, 2005).
Al respecto Sifredo plantea que “la tarea docente de Física puede situarse como un concepto general, que se caracteriza como aquella situación que demanda la realización de acciones y/u operaciones, prácticas o mentales por parte de los estudiantes encaminadas a transformarla” (Sifredo. 2014, p. 4). Por su parte, problema docente de Física, es la tarea, donde el método de realización y resultado son desconocidos por el estudiante a priori, pero que este con la ayuda de deducciones lógicas, acciones matemáticas y el experimento, sobre la base de las leyes y los métodos de la Física está en condiciones de acometer la búsqueda de este resultado o del método que ha de aplicar (Sifredo. 2014, p. 4).
Por otra parte, la Metodología de la Enseñanza de la Matemática en la escuela cubana propone procedimientos y estrategias para la búsqueda de la idea y vía de solución de problemas. Estos problemas pueden ser matemáticos o extramatemáticos, lo común / ellos resulta que quien lo va a resolver no conoce la vía de solución y debe mostrar su empeño en encontrarla. A estos procedimientos y estrategias, por su función de búsqueda, se les denominan heurísticos, en honor a la palabra griega eureka, del mismo significado.
Los procedimientos heurísticos son formas de trabajo y de pensamiento que apoyan la actividad en el proceso de resolución de tareas con alto grado de exigencia mental. Son de gran utilidad para la búsqueda de nuevos conocimientos y para su fundamentación. Ellos, han sido muy estudiados y aplicados en la enseñanza aprendizaje de la matemática en la cual se han obtenido excelentes resultados.
En la última década del siglo XX y los tres lustros del XXI, han sido publicados trabajos relacionados con la heurística en la enseñanza de la Matemática en Cuba: Ballester, S. (1992), Santana, H (1999), Torres, P. (1993, 2000), Castro, N. (1998), Naredo, R. (2000), Cruz (2002), Almeida, B. (2001), Valdivia, M. (2003, 2009, Albarrán, J. (2004), Campistrous L. y C. Rizo (2007). Estos investigadores resaltan la importancia de la heurística y su empleo en los procesos de enseñanza y de aprendizaje de la Matemática en los diferentes niveles educativos, incluyendo la formación de profesores.
Sin embargo, en la enseñanza de la Física en Cuba, las experiencias son más limitadas, (Mondéjar J. y Valdivia, 2004) hace aportaciones en la enseñanza problémica en esta asignatura.
En la formación de profesores en la escuela cubana, se establecen consideraciones conceptuales sobre los procedimientos heurísticos, atendiendo a su clasificación en principios, reglas y estrategias (generales y especiales). Entre los principios heurísticos generales se destacan la analogía, la reducción y la inducción.
Las reglas heurísticas tienen el carácter de impulsos en el proceso de búsqueda de nuevos conocimientos y de la resolución de problemas. Ellas se distinguen de los principios por el alcance de su aplicación, ellas no sugieren directamente la idea principal de solución; pero ofrecen recomendaciones de gran utilidad para llegar a encontrarlas, porque expresan las acciones y operaciones a realizar en la búsqueda de los medios matemáticos y de las vías de solución.
En la clase, estas reglas se pueden utilizar para guiar el pensamiento de los alumnos, ofreciéndolas como sugerencias, indicaciones o en forma de preguntas. Se clasifican, al igual que los principios, en generales y especiales. Las reglas heurísticas generales:
Separa lo dado de lo buscado.
Recuerda conocimientos relacionados con lo dado y lo buscado.
Busca relaciones entre los elementos dados y lo buscado.
Sustituye conceptos por sus definiciones.
Existen otras reglas heurísticas que pueden considerarse especiales porque se refieren a determinados tipos de problemas, por ejemplo, en la resolución de problemas extramatemáticos:
Confecciona una figura de análisis.
Representa las magnitudes dadas y buscadas con variables.
Determina si se tienen fórmulas apropiadas.
Representa las relaciones contenidas en el texto del problema.
Utiliza números más simples en lugar de los números dados.
Reformula el problema.
Las estrategias heurísticas constituyen los procedimientos principales para buscar los medios matemáticos concretos que se necesitan para resolver un problema en sentido amplio y para buscar la idea fundamental de solución, por lo que, se les llama también estrategias de búsqueda.
Existen, además de otras denominadas particulares o especiales, dos estrategias heurísticas que pueden ser aplicadas a cualquier tipo de ejercicio (estrategias generales o universales), ellas son: el trabajo hacia adelante o método sintético y el trabajo hacia atrás o método analítico.
En el trabajo hacia adelante se parte de los datos para realizar reflexiones que han de conducir a la solución de problema, cumpliendo pasos intermedios y en el trabajo hacia atrás se examina primeramente lo que se busca y apoyándose en los conocimientos que se tienen, se analizan posibles resultados intermedios de los que se puede deducir lo buscado, hasta llegar a los datos o a una proposición conocida.
Por otra parte, el Programa Heurístico General es la secuencia de acciones delimitada por las etapas principales del proceso general de resolución de un problema que reproduce la lógica misma de ese proceso. Este programa está compuesto por las siguientes fases y tareas principales:
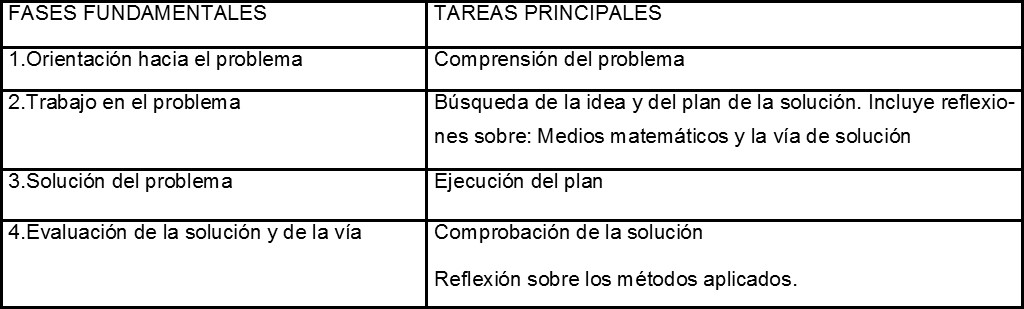
A continuación se presentan dos ejemplos de problemas físicos docentes que aparecen en libros de textos de Física que pueden resolverse empleando los contenidos del Análisis Matemático para su solución, aunque también puedan resolverse por otras vías. Los problemas seleccionados corresponden a la asignatura Física General II, en particular de Cinemática. En cada uno se destacan los contenidos físicos y matemáticos que se emplean, así como los procedimientos heurísticos derivados del Programa Heurístico General (P.H.G.) que se sugieren para la solución.
Problema 1. Cinemática. (1.17: Irodov, 1985)
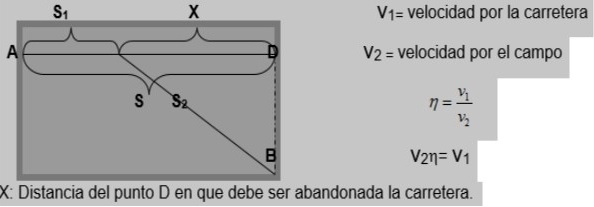
En este problema se aplica el contenido: Extremos de una función del cálculo diferencial del Análisis Matemático, a un problema de contenido físico. Desde el punto A en la carretera hay que llegar en un automóvil en el menor tiempo posible al punto B, dispuesto en el campo a una distancia l de la carretera. Se sabe que la velocidad del auto por el campo es N veces menor que por la carretera.
¿A qué distancia del punto D hay que abandonar la carretera?
PH: Búsqueda de relaciones y dependencias.
EH: Trabajo hacia adelante.
RH: Separar lo dado de lo buscado.
RH: Confeccionar una figura de análisis.
RH: Sustituir conceptos por su definición.
Para conocer a qué distancia del punto D hay que abandonar la carretera, es necesario determinar para qué valor de x el tiempo será mínimo. El tiempo total mínimo es la suma del tiempo que demora en recorrer la distancia S1 más el tiempo que demora en recorrer la distancia S2.
RH: Recordar fórmulas del contenido físico.
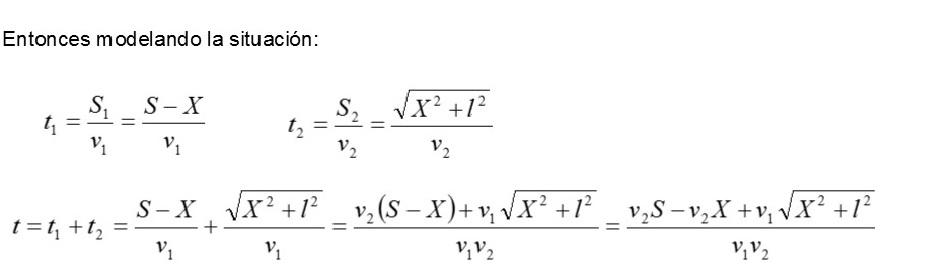
Como S no depende de X, aplicando la condición de mínimo, es decir, determinando la primera derivada de t respecto a X e igualándola a cero, se puede determinar la X que corresponda al tiempo mínimo.
RH: Recordar teoremas del dominio matemático (cálculo diferencial).
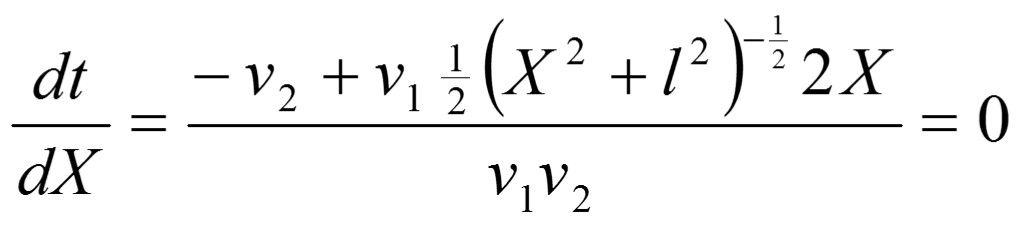
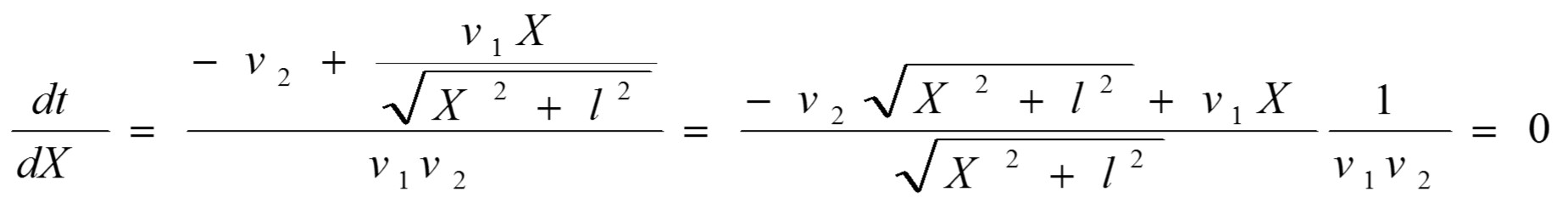

Lo común es que ya se solucionó el problema y se terminó la tarea, pero metodológicamente se debe proceder a la evaluación de la vía de solución encontrada, a través de la comprobación de la solución y la reflexión sobre los métodos aplicados. Esta sería la última fase del Programa Heurístico General donde se pone de manifiesto la dimensión metacognitiva del aprendizaje.
Aplicando el principio de analogía se procede a solucionar el problema siguiente:
Problema 2. Cinemática. (1.22: Irodov, 1985)
En este problema se aplican los conocimientos relacionados con la integral definida al problema inverso de la cinemática. Una partícula se mueve en la dirección positiva del eje X de modo que su velocidad varía según la ley V= (alfa)por X, donde,( alfa) es una constante positiva. Teniendo en cuenta que en el momento t = 0 se encontraba en el punto X = 0, determinar:
a) La dependencia de la velocidad y la aceleración respecto al tiempo.
b) La velocidad media de la partícula en el tiempo, en el transcurso del cual recorre los primeros S metros.

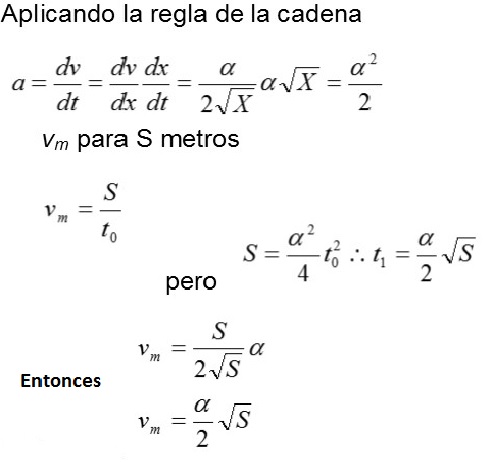
De manera análoga al problema anterior se concluye analizando el resultado.
Esto es una muestra de cómo puede realizarse esta integración en el 2do año, de la carrera a través de las asignaturas Física General I y Análisis Matemático I porque a pesar de la relación que existe en la forma de enseñar ambas, no siempre se aprovechaban esas potencialidades para profundizar y sistematizar los contenidos de gran significado para los estudiantes de la Licenciatura en Educación en el área de las Ciencias Exactas.
CONCLUSIONES
La Física y la Matemática como asignaturas deben estar integradas de manera tal, que el estudiante que se forma como profesor de una doble especialidad en la carrera de Matemática - Física pueda comprender el significado de los conceptos, leyes y procedimientos, entender la esencia de los fenómenos que suceden en la naturaleza y su transformación en un servicio útil y de bienestar de toda la humanidad. Para alcanzar esta aspiración, es necesario que en el proceso de formación, se propicie la reflexión ante problemas de las ciencias a partir de los contenidos ya conocidos, que aportan las distintas asignaturas del currículo.
Es importante reconocer que en ocasiones las limitaciones que existen en el aprendizaje de los procedimientos heurísticos por los estudiantes, son consecuencia, en gran medida, de las dificultades que se presentan en la planificación, organización realización, control y evaluación en la “dirección de la dirección” del aprendizaje.
Si los docentes apelan a la creatividad y a la búsqueda de situaciones atractivas y educativas que contribuyan a la dirección del aprendizaje de los procedimientos heurísticos tanto en las clases de Matemática como de Física, contribuirán a lograr una transformación positiva en los resultados del aprendizaje de los estudiantes, los cuales podrán llgar a aplicarlos conscientemente en situaciones de cualquier índole lo cual será una ventaja indiscutible.
REFERENCIAS BIBLIOGRÁFICAS
Albarrán, J. (2004). Las habilidades pedagógicas – profesionales para la instrucción heurística de la Matemática. La Habana. Tesis en opción al grado científico de Doctor en Ciencias Pedagógicas. ISP “E. J. Varona”.
Almeida, B., Borges J. T. y J. Almeida. (2001). La Heurística: su enseñanza en la formación y capacitación de docentes. En: Memorias Evento COMAT 2001. [CDROM]. Matanzas: UMCC 2001. ISBN 959-160098-4.
Ballester, S y otros. (1992). Metodología de la Enseñanza de la Matemática. Tomo 1. La Habana: Editorial Pueblo y Educación.
Campistrous, L. y Rizo C. (2007). Una didáctica para el tratamiento de situaciones de aprendizaje de la Geometría con un enfoque dinámico en la escuela. ENCE 2007. Holguín.
Castro, N. (1998). Una propuesta de Instrucción Heurística mediante la disciplina geometría. Holguín. 73 h. Tesis de Maestría. ISP “José de la Luz y Caballero”.
Contreras Vidal, J L; Torres Rivera R. y Pérez Martín, B. (2014). La interdisciplinariedad a través de la resolución de problemas para la enseñanza aprendizaje de la Física . En: Didáctica de las Ciencias.
Ershov, Y., (1987): Ciencia, cultura, sociedad. En Ciencias Sociales. Moscú. Nº 2 (68).
Irodov, I. (1985). Problemas de Física General. Moscú: Editorial Mir.
Ministerio de Educación. (2010).Indicaciones metodológicas y de organización. Plan D, carrera de Licenciatura en Educación Matemática Física. La Habana. Material en soporte digital.
Mondéjar, J. y Valdivia, M. (2004). La Heurística en la resolución de problemas. En CDROM. Monografías. Matanzas. 2004. ISBN 959-16-0250-2.
Naredo, R. (1997). La utilización de los recursos heurísticos en la resolución de los ejercicios de demostración y cálculo geométrico en 12 grado. Tesis de Maestría. ISPEJV. La Habana.
Nuñez, J. (1998): Algunas nociones de interdisciplinariedad y los sistemas complejos. La Habana: [s.n.]. Fotocopia.
Perera Cumerma, F. (2000). La formación interdisciplinaria de los profesores de ciencias: un ejemplo en el proceso de enseñanza – aprendizaje de la Física. Tesis en opción al grado científico de Doctor en Ciencias Pedagógicas. ISP “Enrique José Varona”. Ciudad de La Habana.
Pino Batista, M G. (2005). Procedimientos metodológicos para la comprensión de los problemas físico - docentes y la planificación de su resolución en la escuela secundaria básica. Tesis presentada en opción al grado científico de Doctor en Ciencias Pedagógicas. Universidad de Ciencias Pedagógicas”Juan Marinello Vidaurreta”, Cuba.
Sifredo Barrios, C; Rivero Pérez, H R. y González Barreto, M. (2014). La modelación de los problemas físicos. Procedimiento que facilita su solución. En: Didáctica de las Ciencias.
Torres, P. (1993). La enseñanza problémica de la Matemática en el nivel medio general. Tesis para la opción al grado de doctor en Ciencias Pedagógicas. La Habana.
Torres, P. (2000). La Instrucción Heurística de la Matemática Escolar. La Habana. ISP “E. J. Varona”.
Valdivia, M. (2003). La instrucción heurística en el Análisis Matemático en la formación de un profesor de Matemática. Tesis en opción para el Título Académico de Master en Didáctica, mención Matemática. UCP “Juan Marinello”. Matanzas.
Valdivia, M de los A. (2009). Una estrategia didáctica para la dirección del aprendizaje de los procedimientos heurísticos en la asignatura Matemática y su Metodología I de la Licenciatura en Educación en el área de Ciencias Exactas. Tesis en opción al grado de Doctor en Ciencias Pedagógicas, Universidad de Ciencias Pedagógicas “Juan Marinello Vidaurreta”