INTRODUCCIÓN
La formación de profesores de Matemática y Física ha transitado por diferentes modalidades en correspondencia con las necesidades de cada momento. Una valoración integral del problema actual determinó la necesidad de realizar modificaciones sustanciales en el sistema de formación docente para los diferentes niveles de enseñanza, teniendo en cuenta la experiencia histórica y las nuevas condiciones de la educación en nuestro país, lo que ha conducido a la elaboración de los planes de estudio D. En particular se ha entendido necesario pasar de un profesor de Ciencias Exactas responsabilizado con el desarrollo de tres asignaturas, incluida la Informática en el nivel medio superior, a un profesor de Matemática y Física, tanto para la educación media básica como para la superior.
Con este perfil se pretende formar un profesional científico - metodológica, que le permita dirigir el proceso educativo y en particular, el proceso de enseñanza - aprendizaje de la Matemática y la Física con un enfoque interdisciplinario. Así el Modelo del profesional de esta carrera define que el objeto de trabajo del profesional de esta carrera es el proceso educativo y en particular, el proceso de enseñanza – aprendizaje de la Matemática y la Física, en la educación media básica (Secundaria Básica) y media superior (Educación Preuniversitaria, Técnico Profesional y Adultos).
Un profesor de Matemática y Física no puede ser la suma de dos modos de actuación diferentes. No debe tener contradicciones en el desempeño a la hora de asumir una de las tareas típicas del profesor de ciencias. Por otra parte debe ser coherente en el lenguaje que a veces difiere de una asignatura a otra y que está influido por toda la tradición en la enseñanza de ambas ciencias por separado. Por ello la formación de un profesor de Matemática y Física requiere de un enfoque interdisciplinario en el contenido de las ciencias y en sus didácticas, más allá de un acercamiento formal entre ambas asignaturas.
Sin embargo, hay barreras que no favorecen el logro de este objetivo. Los docentes que laboran en la formación de profesionales de la educación, en su mayoría, son graduados de carreras con un perfil, o sea, de una sola especialidad, el plan del proceso docente no satisface las exigencias para la formación de este profesional, los programas de disciplinas se corresponden básicamente con los que se elaboraron para las carreras de formación de profesores de una sola especialidad. Por otra parte, en los programas de disciplinas físicas y matemáticas, se hace referencia a cómo lograr la interdisciplinariedad pero no resulta suficiente.
En este trabajo se pretende contribuir a la sistematización y profundización de los contenidos matemáticos y físicos en la formación de profesores de Matemática y Física mediante la resolución de problemas físicos docentes.
DESARROLLO
En el plan del proceso docente para la carrera de profesor de Matemática –Física se conciben varias disciplinas. Las dedicadas a los contenidos de Matemática y Física son: Álgebra (4 asignaturas), Análisis Matemático (5 asignaturas), Geometría (2 asignaturas), Probabilidades y Estadística (2 asignaturas) y Física General (6 asignaturas). En los programas de disciplina se declara la necesidad del enfoque interdisciplinario en el desarrollo de estas. Este trabajo se enfoca en la interdisciplinariedad entre el Análisis Matemático y la Física General (en particular la Física General I) En la fundamentación del programa de la disciplina Análisis Matemático se plantea:
Este programa debe coadyuvar a la formación integral y profesional de los estudiantes, en especial, al desarrollo de un modo de actuación profesional pedagógico a través de las diferentes formas organizacionales del proceso educativo, al sistematizar y profundizar los contenidos esenciales de la matemática escolar a través de los nuevos contenidos que no solo tienen un carácter sistematizador sino que profesionalmente constituyen nuevos recursos generalizadores dentro y fuera de la disciplina para vincular la Matemática con la vida y otras disciplinas, en particular con la Física, a través de la modelación de problemas cuya resolución se apoye en los recursos informáticos. (Jiménez, 2012, p.3)
Por otra parte, se precisa como uno de los objetivos generales del programa:
Identificar, formular y resolver problemas, incluidos los de demostración o refutación de proposiciones y los que modelen situaciones problemáticas del ámbito social y práctico, que requieran en especial de contenidos físicos, a partir de establecer relaciones de dependencia entre magnitudes variables con abstracción de su contenido, a través del límite, la continuidad, la derivación, la integración y la resolución de ecuaciones diferenciales de primer y segundo orden y en las que en su resolución utilicen métodos exactos. (Jiménez, 2012, p.3)
Sin embargo, en lo expresado solo no se aborda en toda su potencialidad el enfoque interdisciplinario. De la misma manera se manifiesta el programa de Física General. En las Indicaciones Metodológicas Generales se establece que:
Dado las particularidades de la carrera es conveniente dejar establecida la concepción del trabajo con los contenidos de la Matemática dentro de la disciplina. La matemática es el lenguaje de la física, asumiendo como tal un modelo matemático que contiene no solo las estrictas formas y relaciones cuantitativas de los objetos abordados sino portador, además, de un estricto sentido físico. (Jiménez, 2012, p.8)
Las matemáticas están presentes en todo momento durante la conformación de los conocimientos físicos.
En la concepción de los currículos de Física, tradicionalmente ha primado el uso de los métodos matemáticos exactos, lo cual trasmite una visión parcializada del proceso de construcción de la física como ciencia y como disciplina, pues también forman parte ineludible de dicho proceso los modelos matemáticos, dada la información que permiten.(Delgado, 2012, p.19)
La introducción de la interdisciplinariedad implica una transformación profunda en los métodos de enseñanza y requiere de un cambio de actitud y de las relaciones entre los docentes y entre estos y los estudiantes. Se requiere de un profesor que tenga pensamiento interdisciplinar como premisa para que pueda trasmi¬tir esta forma de pensar y proceder a todos sus estudiantes.
La interdisciplinariedad entre el Análisis Matemático y la Física General debe trascender de un mero acercamiento formal y establecer una relación de esencia de ambas disciplina. El autor considera que una vía eficiente para este logro es la resolución de problemas físicos docentes (no se trata de resolver problemas matemáticos que involucren conceptos físicos) que requieran el empleo de los contenidos matemáticos pero que a su vez necesiten solo los contenidos básicos (y esenciales) de física que puedan ser de conocimiento por parte del profesor de matemática.
La concepción de los programas de las disciplinas Análisis Matemático y Física General responde, en buena medida a los programas tradicionales de las carreras Matemática Computación y Física y Electrónica. En ellos no se aprovechan las potencialidades que brinda la formación de un profesor de Matemática Física en cuanto a la necesaria relación entre los contenidos de ambas disciplinas. Un reordenamiento adecuado de la disciplina Análisis Matemático (que es potestad de cada universidad) posibilita que al comenzar la asignatura Física General I, los estudiantes hayan recibido el cálculo diferencial y estén comenzando el cálculo integral, lo que permite la profundización en la impartición de los contenidos de la Física General, la sistematización del Análisis Matemático y la aplicación de este a la física.
Es conveniente la introducción en el curso de Análisis Matemático I de las funciones vectoriales de argumento escalar y su derivación. Este contenido no está explícito en el programa de disciplina pero, contradictoriamente, si para funciones de dos variables. De esta manera se puede tratar con fluidez los problemas directo e inverso de la cinemática.
Es imprescindible también la preparación del profesor de Análisis Matemático en los contenidos esenciales de Física ya sea como autosuperación o en cursos de postgrados. Un curso de postgrado con este objetivo se ofrece por la universidad para los profesores tanto de Física como de Matemática.
Para efectuar este enfoque, previamente deben identificarse los nodos cognitivos de ambas disciplinas. Se asume la definición de nodo cognitivo de Marta Álvarez. Según esta autora “Como tal entendemos un punto de acumulación de conocimientos (conceptos, proposiciones, leyes, principios, teorías, modelos) en torno a un concepto o una habilidad” (Álvarez, 2004, p. 11)
No todos los nodos cognitivos revisten la misma importancia en las disciplinas, así se definen los nodos principales como aquellos que se distinguen por su relevancia cultural o sus aplicaciones a la práctica. De especial importancia será entonces la planificación de tareas que permitan activar estos nodos.”(Álvarez, M., 2004, p. 8)
Desde este punto de vista la relación interdisciplinaria puede ser considerada como una relación sistémica entre disciplinas por objetivos comunes, donde cada disciplina como componente del sistema establece nexos estrechos a fin de lograr el cambio en el nodo interdisciplinario. La interdisciplinariedad física-matemática es esencial para estas ciencias y su enseñanza y en particular para la formación del profesor Matemática y Física. Por una parte en las ciencias físicas, los métodos matemáticos se convierten en métodos principales para la investigación de los fenómenos físicos objeto de estudio. Esta afirmación puede ser evidenciada, en:
La dependencia de una magnitud respecto a otra que se expresa mediante conceptos matemáticos: funciones, límite, derivada, integral, ecuaciones diferenciales.
Los objetos físicos tienen variada forma geométrica, se representan mediante un sistema de coordenadas en el espacio (R^n).
Algunos conceptos y modelos físicos responden a estructuras algebraicas, entre ellas, grupos, anillos, cuerpos y espacios vectoriales.
Nodos cognitivos principales de la disciplina Análisis Matemático:
Función. Límite y continuidad. Derivadas y aplicaciones. Sucesión y series. Integrales. Funciones de dos variables. Límite y continuidad. Derivadas de funciones de varias variables. Aplicaciones. Integrales dobles y triples. Aplicaciones. Ecuaciones diferenciales.
Nodos cognitivos principales de la asignatura Física General I:
Cinemática. Dinámica de la traslación. Trabajo y energía. Cantidad de movimiento. Cinemática y Dinámica de la rotación. Oscilaciones. Gravitación y teoría general de la relatividad. Estática y dinámica de los fluidos. Movimiento ondulatorio. Teoría especial de la relatividad. En la concepción del sistema de clases para la asignatura Física General I debe tenerse en cuenta que en el momento que se imparte esta asignatura los estudiantes ya recibieron o reciben las disciplinas:
Fundamentos de la Física Escolar, donde se trataron los contenidos correspondientes a los cursos de Física de la educación secundaria y media superior, por lo que debe evitarse la reiteración de los contenidos. La diferencia fundamental entre una disciplina y otra está dada por el nivel de profundidad de los contenidos.
Fundamentos de la Matemática Escolar donde los estudiantes sistematizan, profundizan y amplían acerca de los contenidos de la enseñanza media básica y media superior, y se fundamentan desde el punto de vista de la lógica clásica, la teoría de conjuntos, los dominios numéricos, las funciones y la teoría de las ecuaciones, así como de la geometría sintética y analítica del plano.
Análisis Matemático, disciplina de la cual ya se trabajaron los contenidos del cálculo diferencial y paralelamente se estudia el cálculo integral lo que permite la profundización en la Física General I.
El análisis de estos tres precedentes nos permite concebir un enfoque del curso de Física General I que considere los contenidos de Análisis Matemático estudiados por los estudiantes. A continuación se proponen elementos que deben tenerse en cuenta en la concepción del curso y algunos problemas resueltos que ilustran como incluir el Análisis Matemático en el curso para el logro de la profundización en la Física General. Se tomó para ejemplificar el tema I del programa de Física General I que incluye los contenidos correspondientes a la cinemática y dinámica de la partícula. Sugerencias metodológicas:
Comenzar el curso con una conferencia y una clase práctica dedicadas al álgebra vectorial donde se precisen las operaciones con vectores, gráfica y analíticamente.
Presentar la cinemática de la partícula de forma deductiva. A partir de las funciones vectoriales generales para las magnitudes aceleración, velocidad y posición, obtener las correspondientes a los casos particulares para los movimientos con aceleración constante, proyectiles y rectilíneo.
Resolver problemas de cinemática sobre los problemas directo e inverso de la cinemática que incluya el trabajo con vectores, el cálculo diferencial y el cálculo integral.
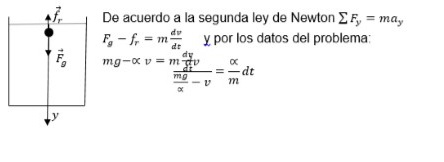
Trabajar la segunda ley de Newton en forma fuerte, la fuerza como derivada de la cantidad de movimiento.
Incluir en los problemas de dinámica los que consideren fuerzas variables, que para su resolución necesiten del cálculo diferencial o el cálculo integral.
A continuación se presentan como ejemplos, un conjunto de problemas físicos docentes que responden a las sugerencias consideradas anteriormente y sus soluciones.
Los problemas se agrupan en correspondencia con los contenidos físicos y se resaltan los contenidos matemáticos que se emplean en cada paso.Problema 1. Cinemática.
Una partícula se mueve de manera tal que el vector posición viene dada por la función :
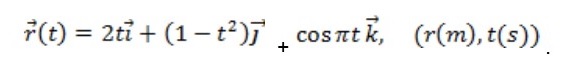 Determine:
Determine:
a)El vector posición para los instantes t= 0 y t= 2s .
b)El desplazamiento entre t= 0 y t= 2s .
c)La velocidad media en ese intervalo de tiempo.
d)La velocidad instantánea como función del tiempo.
e)La velocidad instantánea para t= 2s.
f)La rapidez para t= 2s.
g)La aceleración media en 0 ≤ t ≤ 2s.
h)La aceleración como función del tiempo.
i)La aceleración instantánea para t= 1s.


Resolución:
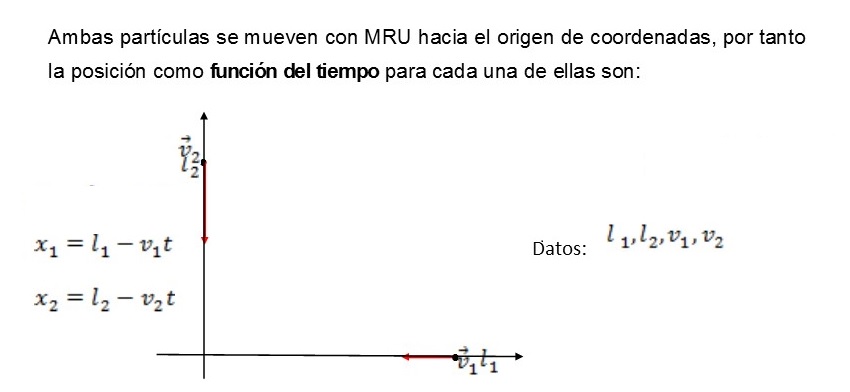





Resolución:

CONCLUSIONES
La formación de un profesor de Matemática Física requiere de un enfoque interdisciplinario que trascienda la formalidad de las exigencias de los programas de estas disciplinas. Una vía para lograrlo es la resolución de problemas físicos docentes que necesiten de los contenidos de la disciplina Análisis Matemático para llegar a la solución. Esto posibilita también elevar el nivel de profundidad del curso de Física General y la sistematización de los contenidos de Análisis Matemático. Se presentan sugerencias metodológicas para el logro de este fin y un conjunto de problemas que responden a estas exigencias.
REFERENCIAS BIBLIOGRÁFICAS
Álvarez, M. (2004). Interdisciplinariedad: Una aproximación desde la enseñanza aprendizaje de las ciencias. La Habana: Pueblo y Educación.
Delgado, L. (2012). Programa de Física General para la Licenciatura en educación Matemática Física. La Habana: Pueblo y Educación.
Irodov. I. (1985). Problemas de Física General. URSS: Mir.
Jiménez, M. (2012). Programa de Análisis Matemático para la Licenciatura en educación Matemática Física. La Habana: Pueblo y Educación.