INTRODUCCIÓN
Tradicionalmente la computadora se ha visto como uno de otras herramientas de los cuales disponen el docente para lograr enseñar los conceptos matemáticos, es decir un recurso didáctico. Pero, ¿realmente su utilización mediante software didáctico será un recurso no indispensable en la enseñanza de la matemática?
Las exigencias actuales de la ciencia y la tecnología requieren una matemática más numérica. Más precisamente, el auge científico y tecnológico ha provocado una evolución de los conceptos matemáticos. Por ejemplo, el concepto de probabilidad no es el mismo que hace 30 años, las computadoras han permitido desarrollar un significado de probabilidad: la probabilidad frecuencial Batanero (2005), útil actualmente para resolver numerosos problemas.
Así, muchos conceptos matemáticos han evolucionado, ¿Y qué ha pasado con su enseñanza? ¿Quizás la enseñanza se ha concentrado, por tradición, en solo una versión desactualizada de los conceptos? En los últimos años, en el caso de Costa Rica, se han hecho esfuerzos importantes por actualizar la enseñanza, pero no han sido suficientes, estos no se han articulado de la mejor manera ni se ha involucrado a los diferentes actores implicados en los procesos de enseñanza-aprendizaje.
Por otro lado, Douady (1984) indica que los conceptos matemáticos tienen carácter de instrumento y carácter de objeto. El ver un concepto como instrumento para resolver un problema es lo que le da sentido al concepto. En dicha resolución, el concepto puede intervenir en uno o varios marcos: geométrico, numérico y algebraico, entre otros. En cada marco el concepto se visualiza en términos de objetos y relaciones, formando significados del concepto en el marco.
El juego de marcos, consiste en establecer correspondencias entre los significados que un mismo concepto adquiere en diferentes marcos. Este juego contribuye a construir la diversidad semántica del concepto, poniendo en evidencia el carácter heterogéneo del conocimiento que varía según el estudiante.
Por lo tanto, Douady (1984) recomienda que, para lograr un buen funcionamiento de los conocimientos en los alumnos, el docente debe elegir problemas donde estos intervienen en dos cuadros como mínimo.
¿Qué sucede en el salón de clases? Tradicionalmente se ha privilegiado el cuadro algebraico. En un inicio esto fue por necesidad, no se contaba con calculadoras potentes (cuadro numérico) ni con software geométrico o programas para graficar (cuadro gráfico). El avance de la ciencia y la tecnológica lo dictó el pensamiento algorítmico.
Sin embargo, en los últimos años el avance de la ciencia y tecnología por medio del desarrollo de software ha permitido que muchos conceptos matemáticos evolucionen, ampliando o robusteciendo su diversidad semántica.
¿Y la enseñanza ha evolucionado? El lugar privilegiado que ha tenido el marco algebraico se ha mantenido, pero quizás ya no por necesidad sino por tradición. Sin embargo, hay otros factores que interviene, como la universalización de la educación vs la accesibilidad a la tecnología en los centros educativos.
Ahora bien, el principal problema es si realmente se cree que es necesario actualizar nuestra enseñanza. ¿Se es consciente de la necesidad del software para lograr comprender la diversidad semántica de ciertos conceptos matemáticos? ¿Qué tan importante es el uso de software en el juego de marcos?
El presente trabajo expone evidencias donde el software se vuelve indispensable para resolución de problemas en un marco determinado.
DESARROLLO
Ejemplos de resolución de algunos problemas.
Ejemplo 1. Una población de ratones, era inicialmente formada por 20 ratones y cada 2 años se triplica la cantidad de ratones. Si hoy se han contabilizado 10 000 ratones. ¿Hace cuánto tiempo aproximadamente se tenía la población inicial de 20 ratones?
Solución.
Sea x el tiempo en años desde que se tenía la población inicial. Así, la cantidad de ratones después de x años es: 20.3x/ 2. Así el problema se traduce en resolver la ecuación: 20.3x/ 2 = 10000.
El concepto de Ecuación invoca una serie de significados según el cuadro en el cual se trabaje. Esta ecuación desde el cuadro algebraico adquiere el significado de ecuación exponencial, esto evoca una serie de procesos algebraicos (herramientas) para resolverla. Desde el cuadro gráfico, la ecuación puede ser vista como hallar las intersecciones de la gráfica de una determinada función con el eje X. El cuadro numérico consiste en ver la resolución de la ecuación se traduce en utilizar una de tantas herramientas, una de ellas es el Método de Bisección. Y desde el cuadro aritmético, la resolución de la ecuación se traduce en realizar cálculos, probando por ensayo y error valores de x hasta lograr la igual.
Seguidamente se exponen algunas soluciones.
Solución algebraica20.3x/ 2 = 10000 ⇒ 3x/ 2 = 500 ⇒x/2 ln 3 = ln 500 ⇒ x ≈ 11 .3136
Note queHace aproximadamente 11 años, 3 meses y 23 días se tenía la población inicial.
Solución numérica-gráficaConsidere la función ƒ(x) = 20.3x/ 2 - 10000. Esta función es continúa. El concepto de que ƒ sea continua se puede transponer a secundaria como una función cuya gráfica no tiene cortes, lo cual involucraría al cuadro gráfico.
Aquí es indispensable el uso de software para graficar ƒ y notar su “continuidad” e investigar donde la gráfica de ƒ corta al eje X. Aquí se presentar dos opciones:
a) Inclinarse más al cuadro gráfico. En Geogebra, por ejemplo, podemos graficar ƒ(x) y luego ir ampliando el eje X para obtener la solución aproximada de 11.31.
b) Inclinarse más al cuadro numérico. Una vez que se verifican gráficamente las hipótesis del Método de Bisección, se procese a aplicarlo utilizando algún software para obtener una solución aproximada tanto como se quiera a la solución real. Por ejemplo, en Sanabria (2007), hay un applet que además de obtener una solución aproximada muestra gráficamente el proceso de cómo se van hallado los puntos de la sucesión.
Solución aritméticaDesde el cuadro aritmético, se procese a probar con valores de x buscando que 20.3x/ 2 se aproxime a 10 000. Realizar este proceso aún con calculadora puede ser tedioso, el software nos ofrece una solución más dinámica:
a) Se puede utilizar Excel y escribir en la celda A2 lo siguiente: “=20*Potencia(3;A1/2)”. Luego se procede a escribir en la celda A1, por ensayo y error, valores de x hasta que la celda A2 brinde un valor cercano a 10 000.
b) En Geogebra, podemos realizar un deslizador llamado x con rango de 0 a 30. El rango luego se puede cambiar según la calidad de la aproximación que se quiera. Así luego se calcula entrada el valor f = 20.3x/ 2 . Se procede a mover el deslizador x buscando que f se acerque a 10 000.
Ejemplo 2. Determine el lugar geométrico determinado por un punto que se mueve de forma que su distancia al eje Y es igual a su distancia al punto (1,1).
El concepto de lugar geométrico adquiere el significado de figura o gráfica en el cuadro geométrico, y de ecuación en el cuadro aritmético.
Solución algebraicaEl lugar geométrico es visto como la ecuación que satisface únicamente aquellos puntos (x,y) que se encuentran en el lugar geométrico.
Sean A(1,1) y P(x,y) un punto cualquiera del lugar geométrico, entonces d(P, Eje Y) = d(P,A)
Por lo tanto,
|x| = √[(x-1)2+(y-1)2] ⇔ y2 - 2x - 2y + 2=0
Así se obtiene la ecuación del lugar geométrico. Dicho de otra forma, se ha obtenido el lugar geométrico desde el punto vista algebraico. (marco algebraico).
Solución algebraica
El lugar geométrico es visto como la gráfica que forman los pares ordenados (x,y) que representan los puntos que se encuentran en el lugar geométrico.
En este caso se utilizará la herramienta "Lugar Geométrico" de Geogebra. Para ello, se debe hallar un punto P del lugar geométrico que dependa de otro objeto en Geogebra. Sea A(1,1). El objeto dependiente puede ser un punto B sobre el eje Y. Así, nos interesa hallar el punto P del lugar geométrico que está en la recta perpendicular al eje Y por B (recta l). Para hallar P, supongamos visualmente que P ya se tiene y se buscan relaciones geométricas que lo definen:
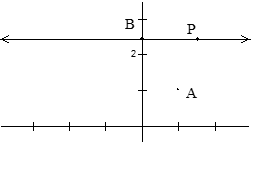
¿Cómo hallar el punto P? Por la definición del lugar geométrico se tiene que d(P,B)=d(P,A), por lo tanto P se encuentra en la mediatriz de AB, basta trazar esta mediatriz y hallar su intersección con la recta l. Así se siguen los siguientes pasos en Geogebra:
- Dibujar: el punto A(1,1), un punto cualquiera B sobre el eje Y.
- Trazar la recta n perpendicular al eje Y por B.
- Trazar la mediatriz m de AB
- Dibujar el punto de intersección de las rectas n y m. Renombrarlo P.
- Se puede activar el rastro de P y mover el punto B, para ver la dependencia de B y parte del lugar geométrico.
- Trazar el lugar geométrico de P al mover B. Se selecciona la herramienta "Lugar Geométrico", el punto P y luego el punto B.
- Ocultar las rectas m y n
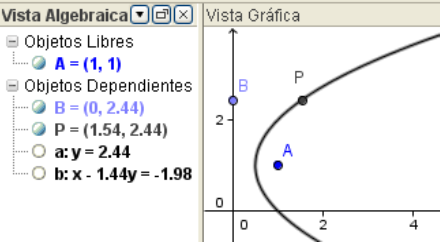
Así, se ha resuelto el problema, se ha hallado la gráfica del lugar geométrico. Dicho de otra forma, se ha obtenido el lugar geométrico desde el punto vista gráfico (marco geométrico).
Sería importante analizar ¿Cuántos docentes consideran la solución geométrica como no válida? Será que inconscientemente privilegian la solución algebraica, pues en su mayoría fueron formados fuertemente en el marco algebraico.
Seguidamente se expone un ejemplo de probabilidad propuesto en Sanabria (2012).
Ejemplo 3 (La bola de fútbol). En un refresco que compró Juan en el local la MINITA, se ganó una bola de fútbol. Sin embargo, al reclamar su premio, la encargada del local le indicó que el premio solamente se lo puede dar el camión repartidor y únicamente pasa el martes entre 10am y 11am aleatoriamente, y en el local se queda exactamente 10 minutos. Dado que Juan está en clases ese día, decide elegir al azar un tiempo entre 10am y 11am para fugarse de clases, y esperar exactamente diez minutos para ver si logra encontrarse con el camión repartidor.
¿Cuál es la probabilidad de que el martes obtenga su premio?
Solución algebraica
En el cuadro algebraico, la probabilidad adquiere el significado dado por la Ley de Laplace: casos favorables entre casos totales.
Considere las variables aleatorias:
- x: tiempo después de las 11 en que llega el Camión, en horas.
- y: tiempo después de las 11 en que llega Juan, en horas.
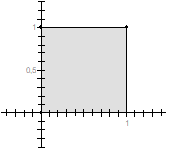
Note que ambas variables varían entre 0 y 1. Así el espacio muestral es
Ω={(x,y) | 0<x<1 y 0<y<1}
En cuanto a los casos favorables, note que se obtiene el premio cuando la diferencia de tiempos de llegada es menor a diez minutos, es decir, a un sexto de hora. Así los casos favorables están representados por el evento
A = {(x,y) ∈ Ω : |x-y| < 1/6}
La representación gráfica de A es:
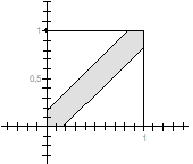
Así, la probabilidad de que obtenga su premio es
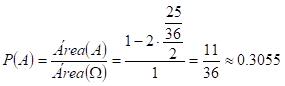
Solución númerica
En el cuadro numérico, la probabilidad adquiere el significado dado probabilidad frecuencial dado por la Ley de los Grandes Números: considere un experimento, si el experimento se repite un número n suficientemente grande de veces, entonces la probabilidad frecuencial de un evento A es el número de veces que ocurre A dividido por n. La probabilidad frecuencial de un evento A es un valor aproximado de la probabilidad de A, que se puede mejorar tanto como se quiera aumentando el valor de n. Actualmente este enfoque ha evolucionado la probabilidad y también su enseñanza donde la computadora es fundamental, como se muestra en Sanabria y Núñez (2010,2011 ).
Se utiliza Excel para modelar el problema. Para ello escriba en las respectivas celdas:
| Celda: |
A1 |
B1 |
C1 |
| Escribir: |
Hora de llegada del camión |
Hora de llegada de Juan |
¿Obtiene el premio? |
| Celda: |
A2 |
B2 |
C2 |
| Escribir: |
=ALEATORIO() |
=ALEATORIO() |
=SI(ABS(A2- B2)<=1/6;"SI";"NO") |
Se interpretará el valor de ALEATORIO() (valor aleatorio entre 0 y 1) como los minutos en horas después de las 10am. Así, si en la celda A2 el valor de ALEATORIO() es 0.15, se tiene que 0.15h=9 min; por lo tanto, la hora de llegada del camión sería a las 10:09 am. Por otro lado, la función ABS(X) devuelve el valor absoluto de X; así, dado que ambos (Juan y el camión) esperan 10 minutos, que equivale a (1/6) de hora, si la diferencia entre las horas de llegada es menor a (1/6), entonces Juan obtiene el premio ese martes; de lo contrario, debe esperar al siguiente. Para simular esta situación 500 veces, como se ha visto, se seleccionan las celdas escritas de la fila 2 y con el mouse se arrastran estas fórmulas hasta la fila 501, obteniendo:
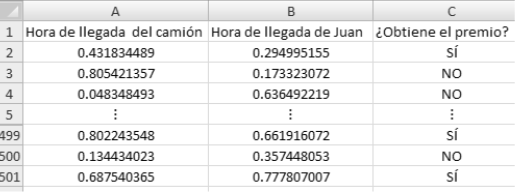
Por ejemplo, en la tercera simulación se tiene que
0.048348493h≈2.90min y 0.636492219h≈38.19min
Entonces, para esta simulación particular, el camión llega aproximadamente a las 10:03 am y Juan a las 10:38 am; por lo tanto, Juan no obtiene su premio.
De las 500 simulaciones, el número de veces que él logra obtener su premio se obtiene escribiendo en una celda vacía:
=CONTAR.SI(C2:C501;"=SI")
En este caso, el valor es de 157. Por lo tanto, la probabilidad frecuencial de que Juan obtenga el premio el próximo martes es de ((157)/(500))=31.4%.
¿Cuántos docentes aceptarían una solución numérica como buena? Quizás no la acepten válida por ser una solución aproximada, pese a que la Ley de los Grandes Números permite acercarnos tanto como se quiera a la solución teórica.
Ejemplo 4. (Problema #5 de la IX Olimpiada Centro Americana y el Caribe, Venezuela 2007) Dados dos números enteros no negativos m y n, con m>n, se dirá que m termina en n si es posible borrar algunos dígitos de izquierda a derecha de m para obtener n. Por ejemplo, 329 termina en 9 y en 29, únicamente. Determine cuántos números de tres dígitos terminan en el producto de sus dígitos.
Solución algebraica
Desde cuadro algebraico, un número tres dígitos es representado en base 10 por (abc) donde a,b,c son sus dígitos. Las herramientas que nos permiten resolver el problema son tomadas de la Teoría de números. Se debe hallar todos los números (abc) que terminan en el producto abc.
- Si (abc) termina en 0, el producto abc=ab·0=0 y hay 9·10·1=90 números, pues a no puede ser 0.
- Como (abc) termina en c. Si abc=c≠0⇒ab=1 ⇒ a=b=1. Hay 9 números.
- Como (abc) termina en (bc). Si abc=10b+c ⇒ b|c∧c|10b, entonces existe un entero k tal que c=bk y como c|10b ⇒ bk|10b ⇒k|10.
- Si k=1 ⇒ b=c ⇒ ab²=11b ⇒ab=11 ⇒⇐ pues a y b son dígitos.
- Si k=2⇒ c=2b ⇒ 2ab²=12b ⇒ ab=6, y se obtiene los números 612,236,326.
- Si k=5 ⇒ c=5b ⇒ 5ab²=15b ⇒ ab=3 y se obtiene 315.
- Si k=1 ⇒ b=c ⇒ ab²=11b ⇒ab=11 ⇒⇐ pues a y b son dígitos.
Por lo tanto, hay 103 números que terminan en el producto de sus dígitos.
Solución númerica
La solución consiste en ir comprobando, por ensayo y error, cuáles de los números del 1 00 al 999 cumplen que terminan en el producto de sus dígitos.
Hacer este proceso a mano puede resultar tedioso, por lo que se debe recurrir a un software para determinar dichos números.
Solución utilizando la programación. Mediante un lenguaje de programación se puede realizar un ciclo que verifique para N=1 00 hasta N=999 si N terminan en el producto de sus dígitos, si esto sucede se agrega un 1 a C que debe iniciar en 0. Hay final del ciclo, C dará la respuesta.
Solución utilizando Excel. Se escribe:
| Celda: |
A1 |
B1 | C1 |
| Escribir: |
Número N |
P= producto de los dígitos de N |
¿N termina en P? |
Luego en la columna A, desde A2 hasta A901, se escriben los números del 1 00 al 999. Para ello basta escribir los primeros dos números, seleccionarlos y con el mouse se arrastra la esquina inferior derecha de la selección hasta la celda A901 .
Para determinar P, note que P es el producto del dígito de las unidades, el dígito de las decenas y el digito de las centenas. Así se escribe en la celda B2:
“=RESIDUO(A1;10)*RESIDUO(ENTERO(A1/10);10)*ENTERO(A1/100)”
Esta fórmula se arrastra hasta la fila 901.
Para saber si ¿N termina en P?, esto sucede si el dígito de las unidades de N es igual a P, o si el residuo de N÷100 es igual a P. Así se escribe en la celda C2:
“=SI(O(RESIDUO(A1;10)=B1;RESIDUO(A1;100)=B1);"SI";"NO")”
Esta fórmula se arrastra hasta la fila 901.
Finalmente, se cuentan cuántos “SI” hay en la columna C. Para ello, se escribe en alguna celda vacía:
“=CONTAR.SI(C1:C901;"SI")”
Obteniendo el resultado.
¿Cuántos profesores consideran la solución aritmética como válida? Curiosamente, el autor de este trabajo fue jefe de la Delegación de Costa Rica en la IX Olimpiada Centro Americana y el Caribe, Venezuela 2007. En esta olimpiada este problema genero polémica pues un estudiante de secundaria al resolverlo hizo una tabla con los números del 100 al 999, verificando uno a uno si cumple o no lo requerido. Al final halló los 103 números. La pregunta valía 7 puntos, ¿merecía los 7 puntos? Obtener los 7 puntos en una pregunta implicaba una mención honorífica para el estudiante.
Realmente la solución es válida, quizás poco elegante aunque se puede volver elegante utilizando software. Quizás lo que falle aquí es la habilidad para detectar cual cuadro me sirve más utilizar, pero esta habilidad (noción protomatemática) no es susceptible de la evaluación.
Para finalizar, piense en un Gauss del futuro (Juan) en la Escuela, donde ante la
interrogante que le hace la maestra: ¿Cuánto es la suma de los números del 1 al
100?, saca su computadora y obtiene el resultado por medio de Excel. Note la
habilidad que tiene Juan para ver que por medio de software puede obtener una
solución rápida y eficiente (solución aritmética). Tan hábil es Juan como el antiguo
Gauss que obtuvo una fórmula para sumar los primeros n números al resolver el
problema (solución algebraica). Pero, Ana fue la más hábil, pues Ana es aquella que
obtuvo la solución de las dos formas, moviéndose en los dos cuadros.
CONCLUSIONES
Se ha evidenciado que el software didáctico se hace necesario para manipular toda la diversidad semántica de ciertos conceptos matemáticos.
En décadas anteriores se privilegió el marco algebraico por necesidad. Con el auge de las tecnologías esto ha cambiado. Sin embargo, es necesario unir esfuerzos y realizar investigaciones para propiciar una actualización de la enseñanza de la matemática adecuada.
Los ejemplos mostrados evidencian un uso distinto de la computadora. No es solo oprimir botones o ver lo que uno ya se imagina. Es una interacción con ella en busca de la solución de un problema. Esto permite fomentar el pensamiento algorítmico, que es una exigencia social de muchas empresas a sus empleados.
Este trabajo es una primera aproximación para evidenciar la necesidad del uso de
software en la enseñanza de las matemáticas. Esta aproximación debe ser nutrida
y complementada con trabajos de investigación. Particularmente, sería importante,
investigar el siguiente efecto de la enseñanza tradicional en los docentes: la solución
válida de un problema es solo la algebraica.
REFERENCIAS BIBLIOGRÁFICAS
Batanero, C. (2005). Significados de la probabilidad en la educación secundaria. En R. Farfán y cols. (Eds.). Relime, 8(3), 247-263. 2005.
Douady, R. (1984). Relación enseñanza –aprendizaje, Dialéctica instrumento – objeto, Juego de marcos. Cuadernos de Didáctica de las Matemáticas Nº 3, IREM de Paris 7.
Sanabria, G. (2007). Tecnologías de Internet: Hacia una propuesta didáctica para la enseñanza de Métodos Numéricos en secundaria. Revista digital Matemática, Educación e Internet [en línea]. Vol. 8, No 2. 2007. [fecha de consulta: 29 Octubre 2015]. Disponible en: www.cidse.itcr.ac.cr/revistamate
Sanabria, G. (2012). Comprendiendo las Probabilidades. Editorial Tecnológica de Costa Rica.
Sanabria, G. & Núñez, F. (2010) Una propuesta para introducir el estudio de las probabilidades: Probabilidad Frecuencial. En Facultad de Ciencias Naturales, Universida Estatal a Distancia. Memorias III Encuentro de Enseñanza de la Matemática UNED, realizado en el INBio Parque, Heredia, Costa Rica, 3 y 4 de setiembre 2010. InBio Parque, Heredia, Costa Rica.
Sanabria, G. & Núñez, F (2011). Introducción a la probabilidad utilizando la simulación en Excel. Memorias del 1er Encuentro Internacional de Enseñanza de la Probabilidad y la Estadística (EIEPE), del 12 al 15 de julio de 2011. México: Facultad de Ciencias Físico Matemáticas de la Benemérita Universidad Autónoma de Puebla.