INTRODUCCIÓN
A partir de la construcción de la parábola como lugar geométrico (ver Figura 1), mediante el uso del software GeoGebra que bajo la asesoría de los autores de este trabajo realizó un profesor de nivel preuniversitario.
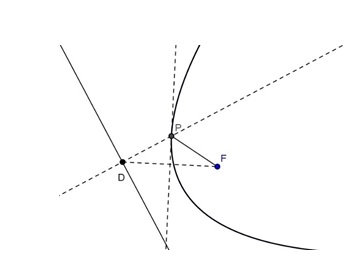 Figura 1. Fuente propia.
Figura 1. Fuente propia.
El profesor preguntó ¿por qué la parábola que se ha construido tiene por ecuación la expresión 9235210000x^2-34855470000xy-304201763100x+32887822500y^2+29584000600y=-810946643309? Cuando los autores del trabajo le sugirieron al profesor fuese más específico en su cuestionamiento, éste mencionó que le causó sorpresa el término -34855470000xy en la ecuación, ya que comúnmente en los textos de matemáticas del nivel preuniversitario las ecuaciones de segundo grado que se presentan y de las que se hacen algunos estudios, son de la forma: Ax^2+Cy^2+Dx+Ey+F=0; en la argumentación del profesor. Cuando se le preguntó sobre la relación que existe entre las ecuaciones Ax^2+Bxy+Cy^2+Dx+Ey+F=0 y Ax^2+Cy^2+Dx+Ey+F=0, se pudo notar que tiene dificultades para argumentar sobre la relación, y en particular, no argumentó sobre cómo transformar ciertas ecuaciones como la del lugar geométrico y llevarlas a las formas que el profesor ha identificado en los textos.
En este cuestionamiento informal que implementaron los autores de este trabajo, también pudo identificarse limitaciones del profesor acerca de las traslaciones y el cómo esta afecta a la expresión analítica y a la gráfica de una curva de segundo grado.
Las limitaciones en las nociones de transformaciones de traslación y rotación que se identificaron en la situación, motivaron a realizar esta investigación de corte teórico-didáctica. Empezando por analizar cómo se presenta el estudio de las ecuaciones de segundo grado y las transformaciones de traslación y rotación en el nivel pre universitario, para después contribuir con una propuesta didáctica.
Las trasformaciones de traslación y rotación. Su tratamiento en el contexto escolar.
Algunas curvas de segundo grado se empiezan a estudiar en los niveles de secundaria, preuniversitario y universitario al menos en México. Una de las actividades que se realizan con las curvas es la graficación, a este respecto se promueven algunos métodos para tal propósito: tabulación, operaciones con gráficas prototipo, método de las operaciones, desplazamientos horizontales y verticales, entre otros.
En el estudio de algunas curvas como las secciones cónicas: parábola, elipse, circunferencia que se empiezan a estudiar en el nivel secundaria y pre universitario, se priorizan aquellas cuya gráfica es simétrica respecto a algún eje coordenado o los dos ejes coordenados y también se estudian algunos casos en los cuales el centro o el vértice no están en el origen.
En este último nivel, se propone además, trabajar algunas secciones cónicas cuyo centro o vértice; en el caso de la parábola no están en el origen (Plan de estudios 2010 del Nivel Medio Superior, Universidad Autónoma de Guerrero, CBTis, COBACH) y como método para su graficación, consiste en utilizar recursos de factorización y/o completando cuadrados perfectos, esto último es posible ya que las ecuaciones que generalmente se tratan son de la forma Ax^2+Cy^2+Dx+Ey+F=0, con A,C,D,E y F constantes.
Sin embargo, dichos métodos se ven limitados cuando se trata de graficar una ecuación de la forma Ax^2+Bxy+Cy^2+Dx+Ey+F=0. A pesar de que las ecuaciones como la antes citada no están explícitamente propuestas en el plan de estudios del nivel pre universitario, consideramos fundamental que el profesor de este nivel deba dominar este contenido matemático y saber de qué manera preparar la actividad de enseñanza. Ya que se considera fundamental en este nivel iniciar los procesos de generalización en el estudio de las ecuaciones de segundo grado y su graficación (Morales, Locia y Salmerón, 2015).
En el nivel superior, en particular, en la Licenciatura en Matemáticas (Plan de estudios, 2009), en la unidad de aprendizaje de Geometría Analítica II se propone el contenido de transformaciones de coordenadas y las gráficas de curvas de segundo grado cuya forma es: Ax^2+Bxy+Cy^2+Dx+Ey+F=0.
Recientemente, se tuvo la oportunidad de trabajar el contenido de transformaciones de coordenadas y la graficación de curvas de segundo grado con estudiantes de segundo semestre de la Licenciatura en Matemáticas, y resulta que de veinticinco estudiantes que asistieron al curso, veintiuno de ellos en un primer momento no encontraron relación entre la transformación de coordenadas y los desplazamientos horizontales y verticales de algunas gráficas, es decir, consideraron estas nociones de forma independiente.
Lo anterior se reflejó en las dificultades y los errores que cometieron al querer utilizar recursos de factorización o completar cuadrados perfectos para transformar las ecuaciones a las formas canónicas que ya conocían, mientras que otros estudiantes, sólo mencionaron que las ecuaciones de traslación y rotación ayudan a transformar las ecuaciones y facilitan la graficación, pero no hicieron algún desarrollo analítico para después predecir o hacer el gráfico de la curva.
Consideramos que esta situación es presentada a raíz de los antecedentes del trabajo con el contenido matemático de este tópico, la formación del profesor, el currículo escolar, es decir, que en los niveles secundaria y pre universitario no se prioriza ni se proponen la trasformación de coordenadas como un medio para favorecer la graficación de las curvas de segundo grado, al menos no explícitamente.
Con el propósito de incidir positivamente en la planeación de la enseñanza de las transformaciones de traslación y rotación, y su uso en la graficación de algunas curvas de segundo grado, es que se presenta una propuesta didáctica dirigida al profesor del preuniversitario para facilitarle herramientas didácticas de corte heurístico para su actividad docente y a la vez, que él explore y redescubra mediante el uso del software, entendiendo este último como es una herramienta poderosa para la geometría dinámica, y en particular para la graficación de curvas de segundo grado por trasformación de coordenadas: traslación y rotación.
DESARROLLO
Fundamentación teórico-metodológica.
Recursos heurísticos.
Torres, P. A. (2013) establece que la instrucción heurística de la Matemática presupone, el conocimiento y empleo consciente de tres tipos fundamentales de recursos heurísticos: los medios heurísticos auxiliares, los procedimientos heurísticos y el programa heurístico general. Aquí enfatizamos en los procedimientos heurísticos, los cuales constituyen recursos mentales de búsqueda que permiten orientarse y obtener la vía de solución durante el proceso de resolución de un problema matemático. A este respecto Jungk (1981) clasifica dichos procedimientos heurísticos en principios, reglas y estrategias heurísticas.
Los principios heurísticos constituyen sugerencias para encontrar directamente la idea de solución principal de resolución; posibilita determinar, por tanto, los medios y la vía de solución, dentro de estos principios heurísticos se identifican: la analogía, reducción e inducción (Müller, 1997). La estrategia que se expone aquí, utilizará la reducción como un principio necesario para la simplificación por transformaciones de coordenadas de algunas ecuaciones de segundo grado.
Las reglas heurísticas actúan como impulsos generales dentro del proceso de búsqueda y ayudan a encontrar, especialmente, los medios para resolver el problema. A este respecto (Müller, 1997; citado en Torres, P.A. 2013) clasifica las reglas heurísticas en generales y especiales.
Las reglas especiales son:
- Si tienes que demostrar la igualdad de longitudes o amplitudes, tratar de encontrar triángulos iguales que contengan esos segmentos o ángulos homólogos.
- Si la figura buscada no te conduce inmediatamente al resultado deseado, trata de obtener, mediante líneas auxiliares, figuras que sean fáciles de construir.
Algunas reglas especiales son:
- El método de lugares geométricos, consistente en determinar al menos dos conjuntos de puntos a los que pertenece el punto buscado y determinar la intersección de ambos conjuntos.
- El método de las transformaciones geométricas que radica en construir una figura que cumpla parcialmente con las condiciones exigidas y después obtener la figura deseada mediante una transformación geométrica.
A decir de la propuesta que se describe más adelante, se hará uso del método de las transformaciones de coordenadas: traslación y rotación, para favorecer la simplificación y graficación de algunas curvas de segundo grado, es decir, con esta acción se transformarán ciertas ecuaciones a las formas canónicas de algunas secciones cónicas.
Las estrategias heurísticas se comportan como recursos organizativos del proceso de resolución, que contribuyen en particular a determinar la vía de solución de la situación abordada. Por ejemplo, el trabajo hacia adelante y el trabajo hacia atrás. El trabajo hacia adelante parte de los datos hasta llegar a la solución de la situación, el trabajo hacia atrás se examina lo que se busca y con el conocimiento actual se analizan posibles resultados intermedios de lo que se puede deducir lo buscado.
El software como recurso heurístico en la actividad de enseñanza y aprendizaje de la Geometría.
Los problemas de enseñanza y aprendizaje de la Matemática en los distintos niveles, han motivado tanto a investigadores como a docentes hacia la búsqueda de nuevas herramientas para incidir favorablemente en los procesos de enseñanza y aprendizaje de la disciplina. Las tendencias actuales sobre la enseñanza de la Matemática han destacado la importancia del uso de la tecnología educativa como una herramienta que favorezca dichos procesos.
Investigadores como (Gamboa, 2007; Marmolejo y Campos, 2012) resaltan la importancia de incorporar el uso de las tecnologías en el trabajo en el aula, ya que estos recursos permiten a los alumnos explorar otros ambientes que favorecen la resolución a las actividades de enseñanza que se le proponen y que, con sólo el uso del lápiz y papel, o la información de los libros de texto, notas de clase, entre otros, les sería difícil de obtenerlas.
Morales, A. (2012) señala que el software GeoGebra es un recurso heurístico que permite, vía la visualización y manipulación; que se identifiquen patrones de comportamientos, propiedades y relaciones en los objetos matemáticos. El investigador considera, además, que se favorecen los procedimientos heurísticos de analogía, reducción, inducción y generalización, por ejemplo, en el estudio de áreas y perímetros de los triángulos; el uso del software permitió hacer el tratamiento de la siguiente situación.
Sea un triángulo cualquiera ABC de área S y un punto P en su interior. Si por P se trazan paralelas a cada uno de los lados, se forman tres nuevos triángulos de áreas S_1,S_2,S_3.
Con el software se determinó que la relación entre los perímetros de los triángulos formados y el triángulo original es que: la suma de los perímetros de los triángulos formados es igual al perímetro del triángulo principal, posteriormente se realizó la prueba matemática.
Se determinó que la relación entre las áreas de los triángulos formados y el original es: el cuadrado de la suma de las raíces de las áreas de los triángulos formados es igual a la medida del área del triángulo principal, de manera análoga al caso anterior; se hizo después la prueba matemática.
Morales, A., Locia, E., y Marmolejo, E. (2014) utilizan el software como un recurso de carácter heurístico para estructurar una estrategia metodológica para la asimilación y fijación del concepto de mediana, una recta notable del triángulo. Los investigadores establecen que con este software se favorece la actividad de enseñanza, pues durante el proceso de solución a los problemas que involucran el concepto de mediana aparecen interrogantes que obligan a madurar la planeación de enseñanza y los dominios del contenido matemático necesarios para tal actividad.
Elementos matemáticos.
A continuación establecemos las definiciones y propiedades de la matemática para hacer el tratamiento de la graficación por trasformación de coordenadas de algunas curvas de segundo grado. Cabe destacar, que durante el proceso de desarrollo de la estrategia se darán algunas argumentaciones sobre las definiciones y propiedades, redescubriéndolas primero al utilizar el software.
Definición 1. Trasformación de coordenadas. Es una operación por la cual una relación, expresión o figura se cambia en otra siguiendo una ley dada. Analíticamente la ley indicada viene expresada por una ecuación llamada ecuaciones de transformación.
Traslación de ejes. La operación de mover los ejes coordenados en el plano coordenado a una posición diferente, de manera que los nuevos ejes sean, respectivamente, paralelos a los ejes primitivos, y dirigidos en el mismo sentido, se llama traslación de ejes coordenados.
Teorema 1. Si se trasladan los ejes coordenados a un nuevo origen 0'(a,b) y si las coordenadas de cualquier punto P antes y después de la traslación son (x,y) y (x´,y'), respectivamente, las ecuaciones de transformación del sistema primitivo al nuevo sistema de coordenadas son x=x´+a,y=y^'+b.
Definición 2. Ecuación general de segundo grado.Es una expresión de la forma Ax^2+Bxy+Cy^2+Dx+Ey+F=0.
Bajo las observaciones que se puedan hacer en la ecuación anterior, en general esta expresión es la definición analítica de una cónica. La estrategia didáctica.
El autor de este trabajo, coincide en que las estrategias deben ser producto de elaboraciones más complejas como las llamadas metodologías. Sin embargo, las estrategias también pueden ser diseñadas en función de la perspectiva del profesor, del alumno o del plan de estudios y principalmente en función del contenido (Morales et al, 2014). Es en este sentido, que se ha considerado una estrategia de carácter metodológico cuya característica principal es la de proveer un método de enseñanza, en el cual los procedimientos heurísticos juegan un papel central para el tratamiento de la graficación de algunas curvas de segundo grado a través de las trasformaciones de coordenadas: la traslación, y utilizando en todo el proceso, el software GeoGebra como un recurso heurístico fundamental.
La estrategia didáctica consta de las etapas que a continuación se indican y se describen: Etapa 1. Preparación de las condiciones para el nivel de partida. En esta etapa, esencialmente se trabajan en un primer momento las trasformaciones de traslación de objetos geométricos (figuras geométricas, puntos, rectas, etc.) en el plano mediante el uso del software GeoGebra. De la traslación, no se le da prioridad en un primer momento la traslación horizontal y vertical, sino que primero se hace la traslación en cualquier dirección, para ello; se hace uso de la herramienta Vector.
Descripción: Se activa la opción Polígono en la barra de herramientas y se dibuja un triángulo ABCcualquiera, se activa la opción Vector y se traza un vector con una magnitud considerada. Se activa la herramienta Trasladar; se da clic sobre el triángulo y sobre el vector en ese orden, y de esa manera se habrá trasladado el objeto según el vector de dirección dado. En la siguiente figura se muestran dos traslaciones del triángulo ABC y su nueva posición; el triángulo A'B'C'.
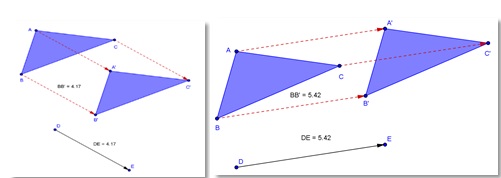
Figura 1. Elaboración propia.
Posteriormente, se cuestiona sobre otras formas de hacer el mismo desplazamiento, el de trasladar el objeto geométrico a cualquier posición del plano.
En la hoja de trabajo de GeoGebra, se activa el sistema de coordenadas rectangulares y manipulando algunas herramientas se redescubre que otra manera de trasladar el objeto geométrico a la posición que actualmente ocupa es a partir de las traslaciones horizontales y verticales.
En esta etapa, se introduce también y se utiliza la opción Animación y se hacen desplazamientos de puntos sobre segmentos, puntos desplazándose horizontalmente y verticalmente. Es importante destacar, que en esta etapa la actividad se centra sólo en la manipulación que se refleja en la hoja de trabajo, es la siguiente etapa, donde se empiezan analizar los comportamientos algebraicos de la traslación.
Etapa 2. Identificación de los efectos de la traslación; a la gráfica y su ecuación. En esta etapa la actividad se realiza esencialmente mediante la ayuda del software; el objetivo principal aquí es identificar qué efectos le ocurre a la gráfica y a su ecuación asociada cuando se realiza una traslación horizontal, vertical o ambas.
Instrucciones: Se inserta en la barra de entrada la expresión y-a=(x-b)^2; donde a y b son valores que recorren intervalos dados; en este caso ambos valores se definen en un intervalo cerrado que va de 0 a 3 y dichos valores se definen con la opción Deslizador en la barra de herramientas del software.
a. Si a=b=0, la ecuación es de la forma y-x^2=0 y su gráfica es la parábola con vértice en el origen. Al configurar la instrucción y al activar el deslizador a mediante la opción Animación se observa que la gráfica de la ecuación y-x^2=0 se traslada horizontalmente del punto origen del sistema coordenado al punto (3,0) y en ese proceso de traslación; la ecuación adquiere distintos comportamientos, algunos de ellos se muestran a continuación: -x^2+0.2x+y=0.01,-x^2+0.4x+y=0.04,-x^2+0.6x+y=0.09,-x^2+0.8x+y=0.16,…,-x^2+6x+y=9 ⇔(x-3)^2-y=0.
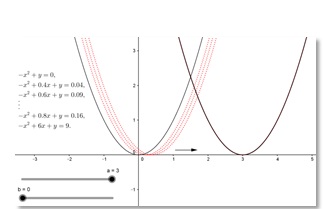
Figura 2: Elaboración propia.
Con la acción realizada, se identifica que cada ecuación de las anteriores es un caso particular de la ecuación de la forma Ax^2+Dx+Ey+F=0, que a su vez, es un caso particular de la ecuación general de segundo grado en dos variables Ax^2+Bxy+Cy^2+Dx+Ey+F=0. Si hacemos el proceso inverso, es decir configuramos la animación que permita al punto a recorrer de 3 a 0, entonces, la parábola se traslada, y su vértice se traslada del punto (3,0) al punto (0,0), y la ecuación adquiere la forma x^2-y=0; que es una caso particular de la forma Ax^2+Ey+F=0.
Desde el punto de vista geométrico, parece ser claro identificar que luego de la traslación, casos particulares de ecuaciones de la forma 〖Ax〗^2+Ey+F=0 se transforman a casos particulares de ecuaciones de la forma 〖Ax〗^2+Dx+Ey+F=0. La actividad se orienta en atención al proceso inverso, es decir, aquí la pregunta fundamental es ¿cómo lograr analíticamente la trasformación de la ecuación de la forma x^2+Dx+Ey+F=0 a la ecuación de la forma 〖Ax'〗^2+Ey'+F'=0?
Analicemos el caso del ejemplo anterior, para transformar la ecuación -x^2+6x+y=9 ⟺(x-3)^2-y=0. Si hacemos x^'=x-3, y reemplazamos en (x-3)^2-y=0, esta última ecuación se transforma en x^'2-y'=0; esta ecuación tiene el mismo comportamiento gráfico que x^2-y=0; tras algunos ejercicios se verifica que se trata de una traslación de un sistema coordenado a un nuevo origen.
b. Si se hace ahora, x^'=x-a y se reemplaza en la ecuación Ax^2+Dx+Ey+F=0; esta última se transforma en la ecuación de la forma A〖x^'〗^2+Ey'+F^'=0; que de igual manera se compara con la expresión 〖Ax〗^2+Ey+F=0. Lo que sigue de este análisis es la formulación de cuestiones que permitan al profesor dirigir su planeación y actividad de enseñanza hacia la generalización y necesidad de formalización desde la matemática de estas ideas. Para el caso de la traslación vertical, se sigue un procedimiento análogo al caso de la traslación horizontal, se pone en cero el deslizador a y se anima el deslizador b, de esta manera se identifican casos particulares de este comportamiento, pues en este caso, solo se ve afectado el término independiente de la ecuación y a partir de aquí, se generaliza la traslación vertical del ejemplo que se ha venido tratando. Así, se si hace y^'=y-b y se reemplaza en Ax^2+Dx+Ey+F=0; ésta última se transforma en la forma Ax^'2+Ey^'+F^''=0.
Veamos ahora el caso de la traslación de la parábola de vértice en el origen cuya ecuación es x^2-y=0 a cualquier parte del plano, en este caso, llevando su vértice al punto (3,3).
A continuación, se muestra la traslación al punto indicado.
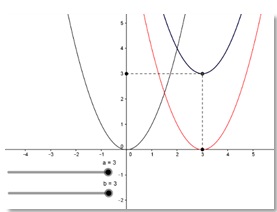
Figura 3: Elaboración propia.
Es importante resaltar que con esta traslación; se identifica que los casos particulares de ecuaciones de la forma Ax^2+Ey+F=0 se transforman a casos particulares de ecuaciones de la forma Ax^2+Dx+Ey+F=0. Generalizando el problema inverso, se tiene que analíticamente las ecuaciones x=x^'+a,y=y^'+b de traslación permiten transformar la ecuación Ax^2+Dx+Ey+F=0 a la forma Ax^'2+Ey^'+F'=0 (1)
Si la parábola abre hacia la derecha o hacia la izquierda, entonces las ecuaciones de traslación transforman la ecuación de la forma Cy^2+Dx+Ey+F=0 a la forma Cy^'2+Dx^'+F''=0 (2)
c. A partir de (1) y (2); se reflexiona y se le da solución a la siguiente pregunta ¿en qué afectan las ecuaciones de traslación a la ecuación de la forma Ax^2+Cy^2+Dx+Ey+F=0? La solución a esta pregunta, permite identificar que las ecuaciones de traslación actuando sobre la ecuación, la transforman a una forma canónica de alguna de las secciones cónicas: elipse, circunferencia, hipérbola, parábola y bajo el conocimiento de las gráficas de éstas, se facilita la representación.
A este respecto Wooton, W., Beckenbach, E. y Fleming, F. (1985), establece que la gráfica de x^2+Cy^2+Dx+Ey+F=0 es una circunferencia, si A=C y en casos excepcionales; puede ser un punto o ∅, es una elipse, si A≠C y A y C tienen el mismo signo y en casos excepcionales; puede ser un punto o ∅, es una parábola, si A=0 o bien C=0 y en casos excepcionales; la gráfica puede ser un par de rectas paralelas, una sola recta o ∅, es una hipérbola , si A y C tiene signos distintos y en casos excepcionales; la gráfica puede ser un par de rectas que se cortan.
Por otra parte, se habrá notado que esta trasformación bajo la traslación prescinde del método de completar cuadrados perfectos, haciendo el efecto de trasladar el origen de coordenadas a otra posición en un nuevo sistema de coordenadas.
Con las ideas anteriores se tienen elementos que permiten identificar los casos de ecuaciones de segundo grado que se han implementado como objeto de enseñanza en el nivel preuniversitario, como las asociadas a las ecuaciones de las secciones cónicas, que si bien para este nivel escolar es propicio este contenido; desde el punto de vista del autor de este trabajo, en este mismo nivel debe explicarse que en efecto las ecuaciones de las secciones cónicas que prescinden del término Bxy son un caso particular de las ecuaciones de segundo grado en dos variables y que su gráfica aparte de estar trasladada puede estar rotada un ángulo θ dado en el intervalo angular válido.
A continuación, se muestra en la siguiente figura casos particulares de ecuaciones de segundo grado; y se identifica que éstas son reducidas mediante las trasformaciones geométricas de rotación y traslación esencialmente; aunque también se indica la completitud de cuadrados perfectos “una práctica tradicional en la enseñanza en el nivel preuniversitario” para la transformación de las curvas de segundo grado a las formas canónicas de las ecuaciones de algunas secciones cónicas.
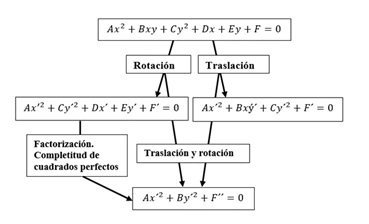
Esquema 1: Elaboración propia.
Etapa 3. Graficación de algunas curvas de segundo grado. En esta etapa se escribe el proceso de graficación de una curva de segundo grado en dos variables, a partir de la traslación de coordenadas.
Este proceso consta de cuatro fases:
i)Se usan las ecuaciones de traslación para reducir la ecuación de segundo grado, que de inicio carece del término de la forma Bxy a una ecuación que carezca de términos lineales.
ii)La ecuación reducida resultante se compara y se lleva a la forma de alguna ecuación canónica de una sección cónica.
iii)Se grafica en un nuevo sistema de coordenadas.
iiii)Se reemplazan las variables del nuevo sistema coordenado por sus equivalentes en términos de las variables del sistema primitivo.
CONCLUSIONES
El trabajo aquí realizado forma parte de un proyecto mucho amplio que está en desarrollo, el cual se ha denominado. “Las transformaciones geométricas en el plano y la graficación de curvas de segundo grado: Una propuesta de enseñanza-aprendizaje basada en el software GeoGebra para el nivel preuniversitario”.
En cada una de las etapas que se han descrito antes; se mostraron algunas ideas de carácter intuitivo (a raíz de la utilización del software como recurso heurístico fundamental) sobre el análisis de los casos particulares de ecuaciones de segundo grado en dos variables y los efectos sobre ellas a partir de la traslación. El objetivo de seguir esta propuesta es con la idea de que en el profesor le surjan interrogantes sobre el tipo de actividades que debe planear para la actividad de enseñanza de la transformación geométrica: traslación y su uso en la reducción de algunas curvas de segundo grado, para luego tratar su graficación. Con ello, él pueda identificar cómo generalizar las formas y los comportamientos; posteriormente, cómo posibilitar métodos no usados tradicionalmente para la graficación en este nivel.
Lo que sigue de este trabajo, es introducir formalmente los conceptos y propiedades que se ponen en juego en este proceso de transformación de las ecuaciones de segundo grado en dos variables y su graficación.
Resulta fundamental destacar que el software GeoGebra como recurso heurístico; posibilita mediante el ambiente dinámico la identificación de efectos a las ecuaciones y a las gráficas asociadas a éstas. El cual permite formular preguntas fundamentales para el estudio analítico y geométrico de las propiedades de las curvas de segundo grado y sus graficación.
REFERENCIAS BIBLIOGRÁFICAS
Gamboa, R. (2007). Uso de la tecnología en la enseñanza de las matemáticas. Cuadernos de investigación y formación en educación matemática 2(3), 11- 44.
Jungk, W. (1981). Conferencias sobre metodología de la enseñanza de la matemática 2. Segunda parte. La Habana: Pueblo y Educación.
Locia, E., Mederos, O., Morales, A., Rodríguez, J. M., y Sigarreta, J. M. (2014). Metodología para los procedimientos de solución de problemas sobre Ecuaciones Diferenciales. Matemática, Educación e Internet 14(2), 1-18.
Marmolejo, J. E. y Campos, V. (2012). Pensamiento lógico matemático con scrath en el nivel básico. Vínculos 9(1), 87-95.
Morales, A., Marmolejo, J. E., y Locia, E. (2014). El software GeoGebra: Un recurso heurístico en la resolución de problemas geométricos. Premisa 16(63), 20-28.
Morales, A. (2012). Estrategia metodológica de carácter heurístico para el estudio de las relaciones de medidas geométricas: El caso de áreas y perímetros. Premisa 14(55), 20-31.
Morales, A., Locia, E., y Salmerón, P. (Noviembre 2015). Recursos heurísticos para la actividad de enseñanza de las transformaciones geométricas en el nivel preuniversitario. En B. Almeida. (Presidencia), Ponencia llevada a cabo en el XVI Evento Internacional “La Enseñanza de la Matemática, la Estadística y la Computación”. Varadero, Matanzas, Cuba.
Plan de estudios (2009). Unidad Académica de Matemáticas. Universidad Autónoma de Guerrero: México.
Plan de estudios (2010). Nivel medio superior de la Universidad Autónoma de Guerrero: México.
Torres, P. (2013). La instrucción heurística en la formación de profesores de Matemáticas. En Dolores, C., García, M., Hernández, J. A., Sosa, L. (Eds.). Matemática Educativa: La formación de profesores (pp. 205-221). Díaz de Santos.
Wooton, W., Beckenbach, E. F. y Fleming, F. J. (1985). Geometría Analítica Moderna. México: Publicaciones cultural S. A. de C. V.