INTRODUCCIÓN
La educación matemática a temprana edad ha sido una parte importante de los jardines infantiles y de la pre escolaridad durante los últimos 200 años (Balfanz, 1999, p. 3-10). Destaca en esta línea lo propuesto por Montessori (1964), la cual desarrolló una serie estructurada de actividades matemáticas para desarrollar habilidades en niños pequeños. La educación en matemáticas se hace parte desde los inicios, con la intención de que todo ser humano desarrolle ciertas habilidades y conozca algunos elementos básicos de la matemática de manera adecuada.
Algunos estudios (Baroody, Lai y Mix, 2006; Clements y Serama, 2007; Ginsburg, Cannon, Eisenband, y Pappas, 2006) muestran que alrededor de los cinco años, los niños desarrollan una “matemática del día a día”, la cual incluye ideas informales sobre más y menos, quitar, sobre la forma, el tamaño, la ubicación y posición. En cuanto al desarrollo de las habilidades matemáticas y en esa dirección, nos hemos planteado la siguiente pregunta: ¿Qué habilidades matemáticas y a qué nivel se pueden potenciar estas en niños de aproximadamente cinco años? ¿qué hacemos en la primera infancia para potenciar o desarrollar las bases de este desempeño de habilidades matemáticas? Estas son algunas de las interrogantes que han impulsado los encuentros informales con docentes del área de la educación, en particular con profesionales del área de la educación en matemática, didactas y pedagogos.
Ha sido un largo camino profesional de preguntas sin respuestas precisas, basado principalmente en vivencias, observaciones de aula y el compartir durante más de 30 años con pre-escolares, lo que ha motivado esta investigación. Comenzando con el enfoque metafórico (Soto-Andrade, 2007a; 2007b; 2011, 2012; Soto-Andrade y Reyes-Santander, 2011), considerando un modelo para el pensamiento matemático presentado en Reyes-Santander, (2012), para luego llegar a la corporización de aprendizajes considerado en Luci (2014) se muestra como estos encuentros formales y las discusiones con docentes de educación matemática han generado diseños de clases, las cuales han sido implementadas y analizadas con los marcos mencionados anteriormente.
DESARROLLO
Fundamentos teóricos
Los fundamentos teóricos que se consideran para comenzar con una educación matemática a temprana edad son los estadios de Piaget (1965) relacionadas con el enfoque metafórico, que se complementan con una caracterización del pensamiento matemático (Reyes-Santander, 2012).
Más aún, estos dos troncos teóricos son las primeras articulaciones para un futuro análisis de nuestras experiencias con niños de 5 a 6 años.
Estadios de Piaget
a) Estadio sensorio-motor (recién nacido a 2 años)
b) Estadio de las operaciones concretas (2 a 11años)
c) Estadio de las operaciones formales (11 hacia adelante)
Esta diferenciación, ya nos marca un sendero a considerar antes de la edad de escolaridad formal. Además, considera una subdivisión (a, b y c) de la cual observaremos la b), que es a la que nos referiremos en este trabajo;
En el estadio de operaciones concretas (2 a 11 años), se distinguen dos sub-períodos:
el pre-operacional (2 a 7 años).
operaciones concretas (7 a 11 años).
De estos dos sub-períodos, nos interesa el pre-operacional de 2 a 7 años en donde se sitúan nuestros estudiantes de 4 a 6 años y cuyas experiencias se desarrollan en sus grupos de pre-escolar.
En la búsqueda de antecedentes que complementen lo anterior y que además amplíe las miradas para comprender de mejor manera nuestras interrogantes, consideramos a Lastra (2010) cuando se refiere a que mientras más interacción social, más conocimiento, más posibilidades de actuar -y por ende-, se realizan funciones mentales más potentes en el individuo. El desarrollo de éste, llega a su plenitud en la medida en que se apropia -es decir que hace suyo-, o interioriza las habilidades inter sicológicas. En principio, dependerían de los otros; en un segundo momento –y a través de la interiorización-, el individuo adquiriría la posibilidad de actuar por sí mismo y asumiría la responsabilidad de su propio actuar.
Las fortalezas de la teoría de Vygotsky (1988;1995) se reflejan en:
- Las habilidades cognitivas de los niños son más comprensibles, cuando se analizan, se estudian sus orígenes y sus transformaciones.
- Estas están mediadas por la palabra, el lenguaje y el discurso como formas de representaciones de ideas y conceptos, de comunicaciones. También como herramientas psicológicas para la transformación de la actividad mental.
- Y tienen su origen en las relaciones sociales y están inmersas en una transformación cultural.
Lastra (2010) destaca que en este período de la educación infantil de niños/as desde los primeros años hasta el final de la primaria, es decisivo, para los aprendizajes matemáticos fundamentales, así como la formación de la actitud positiva o negativa hacia la matemática.
Esta área afectiva -en cuanto se refiere a actitud positiva-, ha sido considerada cada vez con más fuerza y mayor presencia en investigaciones del área de la educación matemática. Uno de sus más prominentes representantes Hannula (2012), hace referencia a lo largo de su trabajo de la importancia de considerar el aspecto emocional como apoyo fundamental en el proceso de aprendizaje matemático infantil.
En la misma dirección anterior Sixte y Sánchez (2012), proponen respecto al proceso de interacciones en el aula una necesidad de realizar un análisis de la interacción educativa molecular y exhaustivo de los procesos cognitivos, motivacionales y emocionales, en 'contexto' y 'tiempo' real, lo que se traduce en este trabajo como otro elemento considerado en este trabajo, a saber, la relevancia de la función docente en aula. Nadie puede negar que, a diario, se realizan grandes esfuerzos en las escuelas porque los estudiantes reciban una mejor educación y sobre todo que respondan de buena manera a las expectativas de las mediciones internacionales, que cada vez son más exigentes.
Este aspecto emocional se convierte en soporte fundamental del proceso cognitivo del niño/a en cuanto a su relación con las matemáticas se refiere. Para atender y complementar de mejor manera esta idea, hemos considerado a las Metáforas y la cognición corporizada.
Según Soto-Andrade (2007b): La cognición hecha cuerpo, llamada también “cognición corporizada” es una noción fundamental en ciencias cognitivas contemporáneas. Alude al hecho que nuestro conocer no es un simple percibir una realidad objetiva “allí afuera” ni tampoco un procesamiento de información captada por nuestras ventanas sensoriales, sino que un proceso que se construye a partir de nuestra experiencia corporal sensorio motriz.
Parafraseando a Cardoso y Cerecedo (2008), en cuanto se refiere a la competencia de reunir información sobre criterios acordados, representar gráficamente dicha información y la interpretación de ésta -en la primera infancia-, es preciso iniciarla a partir de la propuesta de códigos personales por parte de los/as estudiantes para, consecutivamente, acceder a los convencionales para representar la información de los datos, es decir, nuestra propuesta es que sea por medio de metáforas y en un proceso cognitivo corporizado.
Pensamiento matemático y cognición corporizada
Se entiende por pensamiento humano, como un compromiso interno, activo, que se hace a través de imágenes internas, utilizando términos lingüísticos internos, representaciones pictóricas y otros contenidos mentales. Pensar en este contexto, tiene el fin de obtener nuevos conocimientos y esto se obtiene solo en las actividades que no están orientadas a las rutinas automatizadas. Al momento de pensar, se utilizan símbolos, imágenes y movimientos, estos son utilizados y relacionados unos con otros al momento de pensar, de manera consciente y/o inconsciente (Asanger y Wenninger, 1999). Además, estos símbolos pueden tener reglas predeterminadas, o bien, estas reglas pueden ser creaciones propias de el/los individuo/s. De esta forma se crea un mundo abstracto de pensar y una realidad personal. El ser humano piensa a través de conceptos, que son representaciones universales y abstractas de los objetos. Estos símbolos, imágenes y conceptos representan un hecho, un objeto, una acción, que son utilizados y relacionados al momento de pensar (Reyes-Santander, 2012).
El pensamiento matemático (PM), es un producto final de variados procesos neuropsicológicos, estos procesos provienen y se desarrollan en diferentes áreas y requieren de diferentes habilidades del individuo. El PM es un producto de la integración de distintas modalidades sensoriales y cognitivas (Reyes-Santander, 2012).
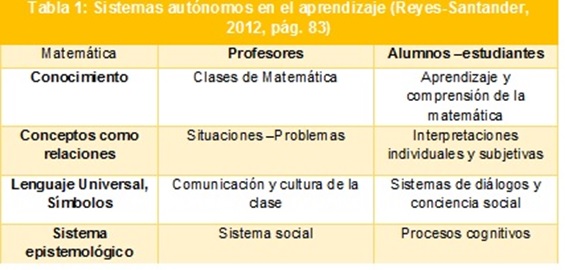
Cada una de las tres áreas que se ven en la tabla 1, representa un sistema autónomo y auto referencial, en el caso de la educación matemática a temprana edad, el sistema autónomo matemático, es considerado como “matemática del día a día”, el otro sistema de alumnos y estudiantes está en su primera etapa de las operaciones concretas (Piaget, 1965), lo cual indica que se debe mirar el pensamiento matemático desde ese punto de vista.
En la tercera columna, se puede observar la relación con lo propuesto por Vygotsky (1995), donde la conciencia social es el puente entre el conocimiento matemático estructurado y la construcción del conocimiento como constructo social.
El pensamiento matemático caracterizado en Reyes-Santander (2012), a utilizar en este trabajo y en relación a los tres sistemas presentados en la tabla 1, se puede describir según la autora (pág. 270): como un proceso cognitivo activo que involucra actividades neurológicas, que comprometen un diálogo interno, que relacionan y utilizan representaciones de todo tipo, capacidades racionales y no racionales, capacidades desarrolladas o por desarrollar y conocimientos almacenados en la memoria. Este proceso está relacionado con la vivencia de situaciones novedosas e interesantes para el individuo y con la búsqueda de respuestas a problemas, que determina el individuo de forma personal, con el objetivo de crear conocimiento sobre el medio que lo rodea y de esta forma construir un mundo matemático individual, con conexiones propias y con sistemas propios de llamados del conocimiento.
Más aún, el modelo del pensamiento matemático está dado por cuatro dimensiones, que están agrupadas desde su procedencia cognitiva y desde su estructura:
- La percepción donde se destacan, la percepción del movimiento, del tiempo, del espacio. En educación matemática temprana también se pueden observar los inicios de la percepción dinámica y estática de los objetos. Considerando en esta etapa del ser humano varios sentidos del ser humano (Steiner, 2009), ya que mientras más estímulos se tengan a esta edad, mayor será el desarrollo de los sentidos del niño pre-escolar.
- Los pensamientos relacionados con los contenidos matemáticos, que a su vez contempla 6 categorías.
- Las estrategias y los procedimientos, que provienen del desarrollo del individuo con el contenido y el medio. En esta dimensión se pone en juego el conocimiento y por lo tanto nuevamente la memoria tiene un papel cognitivo relevante, así como también las capacidades que son puestas en marcha en la búsqueda y desarrollo de un plan.
- Las capacidades no racionales, que provienen del desarrollo de actividades no racionales. Esta dimensión involucra aspectos como la intuición, la creatividad, el sentido común y la fantasía.
Esta caracterización del pensamiento matemático (PM) permite, por un lado, incluir a la percepción, como una componente importante, a considerar en el desarrollo del PM, en cualquier etapa del desarrollo.
La figura 1 muestra las dimensiones del PM y sus categorías, las cuales a su vez forman parte de una relación tetraédrica entre ellos, esto quiere decir, que ninguna de estas componentes esta sobre alguna de ellas y que su relación con las otras tiene el mismo peso. Lo que finalmente se pretende con este modelo es que estas dimensiones y categorías deben estar en equilibrio en nuestras clases de matemática, se deben desarrollar estas cuatro componentes a la vez. En el centro están los medios de comunicación, de los que dispone el ser humano y que deben ser utilizados en todo momento.
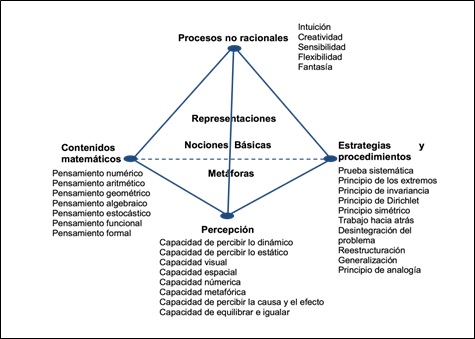
Figura 1: Modelo Tetraédrico del Pensamiento Matemático (Reyes-Santander, 2012, pág. 281)
La percepción, los contenidos matemáticos y los medios de comunicación, pueden ser relacionados a través de los tres niveles de Bruner (1971), enactivo, icónico y simbólico, lo que también da paso al desarrollo de estrategias en todos estos procesos, estarán en juego las capacidades no racionales, todas estas consideraciones, hacen de la educación “encarnada” una posibilidad real y accesible mediante el cuerpo para todos y todas las estudiantes.
Finalmente, esta caracterización y el modelo son utilizados para generar clases que incluyen la percepción como elemento principal en el desarrollo de habilidades, para analizar lo que ocurre en una clase y para visualizar el desarrollo del pensamiento matemático a temprana edad.
Matemáticas en la Educación Inicial
La aproximación metafórica, el aprendizaje corpóreo y el desarrollo del pensamiento matemático, plantean las siguientes ideas centrales para la matemática en la educación temprana:
Los conceptos matemáticos van siempre muy ligados a la experiencia sensorial.
Tener en cuenta la dimensión evolutiva de la adquisición de los conceptos básicos sobre los que se sustentan las nociones y operaciones aritméticas.
Por muy pequeño que sea el niño siempre cuenta con nociones y habilidades previas referidas a lo matemático, de las cuales se debe partir.
Experiencias
Las siguientes experiencias muestran como el desarrollo del pensamiento matemático a temprana edad permite a los estudiantes buscar y compartir dentro y desde sus propias vivencias, mediante el uso de su cuerpo, las respuestas o significados de conceptos y nociones matemáticas iniciales.
A continuación, damos una breve descripción de las actividades que se realizaron en aulas de diferentes colegios y Jardines de Infantes en Santiago de Chile, con diferentes docentes, estudiantes de pre grado cuarto año de la carrera de Educación de Párvulos y también de Educadoras en ejercicio normal de su profesión para que ellas a su vez trabajaran con niños y niñas de 5 años insertos en el sistema escolar.
Actividad 1: “Nociones geométricas iniciales, las figuras, los polígonos”, comentar en voz alta las figuras geométricas que conocen, identificar diferencias entre las figuras; número de lados, de vértices, lados rectos o curvos. Armar diferentes polígonos que emergen de cantidad de nudos al azar, trabajo individual y en grupo. Como material de trabajo se utilizan restos de cuerdas o lanas.
En la figura 2 se muestra el trabajo con niño/as de 5 años, tomando del relato a las/os estudiantes del método de los nudos utilizado por los egipcios para noción de área y perímetro (para controlar sus posesiones). La propuesta moviliza a las/os estudiantes desde el inicio. Cada una/o hace diferentes cantidades de nudos y arma diferentes polígonos, intercambiando con el grupo los elementos representados e identificados.

Fig. 2: Con cuerdas y nudos para representar vértices y lados.
Actividad 2: Denominada; “Nociones geométricas iniciales, los cuerpos geométricos o 3D”, el material se compone de cajas recicladas, goma eva, papel engomado, pajillas de bebida, restos de cuerdas o lanas, trozos de cartulinas de colores y plastilina que se usan para;
Tarea 1: Manipular y caracterizar elementos de una figura 3D o cuerpo geométrico.
Tarea 2: Esta tarea consiste en observar el entorno, describir cuerpos geométricos, destacar características que se encuentran en ellos. Luego se revisan los materiales y el estudiante escoge entre ellos los que le gustan y que le servirán para “imitar” uno de los cuerpos descrito. Manipula y arma un “esqueleto” de un prisma de base triangular con las pajillas, luego marca los vértices con plastilina y completa con las caras de colores en cartulina, finalmente el estudiante comenta todo lo que hizo con su grupo.

En la figura 3 se puede apreciar a un estudiante de 5 años, manipulando un cuerpo geométrico, armado por él mismo con materiales de desecho, recorre con sus dedos las aristas y los vértices verbalizando con el grupo de trabajo, cada elemento que reconoce.
Actividad 3: Denominada; “Nociones matemáticas iniciales, número, antecesor, sucesor, adición y sustracción”. Materiales; goma eva, papel engomado, trozos de cartulinas, plumones de colores, tizas de colores, crayones.
Tarea: En cualquier espacio parejo de un aula de clases o en el patio de la escuela, solicitar a las/os estudiantes que realicen varias marcas que tengan una distancia igual entre ellas. La unidad de referencia será establecida entre las/os integrantes de cada grupo, se marca, se fabrican números con cartulinas, plumones y/o crayones. Los números se ordenan de acuerdo a las instrucciones de orden creciente de izquierda a derecha, marcando el inicio de la recta numérica del piso con el 1 donde el grupo decida, aunque no es requisito que éste sea el primer espacio de la recta.


4a. Colegio 1.
kínder (5 años)Fig. 4b Colegio 2.
Recta numérica corporizada. Desplazamientos corporales.Se dictan números al azar en voz alta, los estudiantes eligen a un representante que se para sobre el número indicado, luego se hacen preguntas de ingenio para motivar la adición o sustracción. Ejemplos: Si el conejo que vive en la casa 4 avanza 3 más… ¿qué número tiene la casa donde llega?, si estamos en el paradero 9 de la micro y me tenía que bajar en el paradero 5, ¿cuántas paradas debo retroceder?
En la figura 4a y 4b se muestra el trabajo con niño/as de 5 años, el cual consiste en desplazamientos corporales sobre una recta numérica representada en el piso de las aulas de clases. Las y los niños y niñas se mueven hacia la derecha cuando avanzan y hacia la izquierda cuando retroceden. De esta manera se integra además las nociones iniciales de adición y sustracción en el ámbito numérico del 1 al 10, que corresponden a sumar como avanzar y restar como retroceder.
De esta manera se produce tal como menciona Luci (2014) una modificación del paradigma de “cómo enseñar”, ya que la Educadora en vez de enseñar un contenido específico, lo que hace es “proponer maneras de cómo se puede aprender”, asegurándose de proponer ambientes de aprendizajes. Esto desarrolla otras capacidades de relación con el aprendizaje matemático, como actuar, comunicar, equivocarse y volver a intentar hasta reconocer que hay más de un camino para llegar al resultado “correcto” de alguna situación problema planteada.


Fig. 5a
Representación de cantidades y adición con ábaco chino del 2 al 9 con niños y niñas de Kínder (5 años).Fig. 5b
Demostración de la docente para comparar con las/os estudiantes.En la figura 5a se muestra el trabajo con niño/as de 5 años de representación de cantidades y adiciones con ábaco chino. Las/os estudiantes manipulan las cuentas del ábaco, diferenciando que debajo de la línea de trabajo se encuentran los valores unitarios y que sobre la línea valen 5 veces. Esto promueve rápidamente la abstracción, la diferencia de valor relacionada con la posición y la introducción del concepto de quinquena (cinco juntos).
En la figura 5b se muestra el trabajo de ejemplificación de la representación de cantidades y adiciones con ábaco chino, con las/os niño/as de 5 años mientras trabajan en grupos. De esta manera se confirman las respuestas individuales y se comentan entre las/os estudiantes y los métodos de búsqueda de solución.
CONCLUSIONES
En las experiencias realizadas se pudo constatar que las/os estudiantes utilizan con mucha naturalidad todas las herramientas que les provee su cuerpo, tal como lo plantea Soto-Andrade (2007a). Manipular, armar, observar, comentar, etc., es decir que no les limita como el papel y lápiz en donde generalmente se les solicita que dejen registro gráfico de los resultados a los problemas planteados, con esto se tiene un desarrollo del PM en su dimensión percepción y desarrollo de estrategias. Mediante las corporización individual, cada estudiante manifiesta los elementos que identifica, relacionándolos con la tarea propuesta por el/la docente.
Las respuestas que son entregadas por las/os estudiantes son muy variadas, ya que éstas dependen directamente del modo personal en que se busca la solución. Esto no significa que sean incorrectas, ya que al verbalizar con su grupo cada estudiante aporta con distintos elementos, así la respuesta se construye, se ajusta, se corrige sin descalificaciones personales al trabajo individual.
Considerar que los programas curriculares, textos escolares y formatos de clases, son rígidos y exclusivos agota tanto al estudiante como al docente. Sin embargo, esta propuesta de aprendizaje promueve la búsqueda de respuestas, por lo tanto, las consultas, los comentarios y la ampliación de conceptos básicos se dan de manera libre y variada, aportando a un aprendizaje más significativo.
El atreverse a Metaforizar y Corporizar nociones matemáticas iniciales se convierte en una eficaz herramienta de aprendizaje, sobre todo en primera infancia donde lo natural es lo espontáneo, lo lúdico y el movimiento, tales elementos ausentes en lo “tradicional y estructurado”.
Considerar solo los sistemas correspondientes a la cultura donde se vive, no hace más que esquematizar las mentes infantiles, establecer creencias erradas de que existen métodos estándares para resolver los desafíos matemáticos. Sin embargo, hacer paralelos entre culturas diferentes y desconocidas aportan a la imaginación e invitan a jugar a ser diferentes, sin quitar la seriedad de los conceptos a aprender.
REFERENCIAS BIBLIOGRÁFICAS
Asanger, R., Weniger, G. & Bertram, M. (1999). Handwörterbuch Psychologie. 4ta edición, Psychologie Verlags Union.
Balfanz, R. (1999). Why do we teach children so little mathematics? Some historical considerations. En J. V. Copley (Ed.), Mathematics in the early years. Reston, VA: National Council of Teachers of Mathematics. 3-10
Baroody, A. J., Lai, M., & Mix, K. S. (2006). The development of young children’s early number and operation sense and its implications for early childhood education. En B. Spodek & O. Saracho (Eds.), Handbook of research on the education of young children. Mahwah, NJ: Erlbaum. 2, 187-221.
Bruner, J. (1971). Toward a Theory of Instruction. 5ta edición. Cambridge: The Belknap Prees of Harvard University.
Cardoso, E. y Cerecedo, M. (2008). El desarrollo de las competencias matemáticas en la primera infancia. Revista Iberoamericana de Educación ISSN: 1681-5653 n.º 47/5 – 25 de noviembre de 2008, EDITA: Organización de Estados Iberoamericanos para la Educación, la Ciencia y la Cultura (OEI).
Clements, D. H., & Serama, J. (2007). Early childhood mathematics learning. En F. K. Lester (Ed.), Second Handbook of Research on Mathematics Teaching and Learning. New York: Information Age Publishing. 461-555
Ginsburg, H. P., Cannon, J., Eisenband, J. G., & Pappas, S. (2006). Mathematical thinking and learning. En K. McCartney & D. Phillips (Eds.), Handbook of Early Child Development. Oxford, England: Blackwell. 208-229.
Hannula, M. (2012). Emotions in problem solving, en 12th International Congress on Mathematical Education, Regular Lecture, Seoul, Corea (pp. 938-957).
Lastra, S. (2010). “La formación del pensamiento matemático del niño de 0 a 4 años” Santiago: Universidad de Chile.
Luci, G. (2014). Metáforas y emociones en el proceso de enseñanza-aprendizaje de las nociones matemáticas iniciales. Trabajo final para optar al Grado de Magíster en Didáctica de la Matemática. Pontificia Universidad Católica de Valparaíso, Chile.
Montessori, M. (1964). The Montessori Method (A. E. George, Traducción). New York: Schocken Books.
Piaget, J. (1965). The stages of the intellectual development of the child. Educational psychology in context: Readings for future teachers, 98-106.
Reyes-Santander, P. (2012). Caracterización del Pensamiento Matemático: Escenarios con estudiantes universitarios y de liceo utilizando temas de la Teoría de Grupos (Doctoral Dissertation). Retrieved from:http://opus.bibliothek.uni-augsburg.de/opus4/frontdoor/index/index/docId/2627
Sixte, R. y Sánchez, E. (2012). Cognición, motivación y emoción en la interacción profesor-alumno. Una propuesta para analizar su relación mediante el registro de las ayudas frías y cálidas, Infancia y aprendizaje, 35, 4: 483-496.
Soto-Andrade, J. (2006). Un monde dans un grain de sable: Métaphores et analogies dans l’apprentissage des mathématiques, Annales de Didactique et de Sciences Cognitives, (11), 123-147.
Soto-Andrade, J. (2007a). Metaphors and cognitive styles in the teaching-learning of mathematics. In D. Pitta-Pantazi, & J. Philippou (Eds.). Proceedings CERME 5 (pp. 191-200). Retrieved 8.3.2008, from http://ermeweb.free.fr/CERME5b/ Descargado: 2012-10-01.
Soto-Andrade, J. (2007b). La cognición hecha cuerpo florece en metáforas, A. Ibañez, y D. Cosmelli, (Editores), Nuevos Enfoques de la Cognición: Redescubriendo la dinámica de la acción, la intención y la ínter subjetividad (pp. 71 -90. Chile. Universidad Diego Portales.
Soto-Andrade, J. y Reyes-Santander, P. (2011). Conceptual metaphors and “Grundvorstellungen”: a case of convergence? In: M. Pytlak, T. Rowland, & E. Swoboda (Eds.), Proceedings of CERME 7 (pp. 735- 744), Rzészow, Poland: University of Rzészow.
Soto-Andrade, J. (2012). Metaphors in Mathematics Education. In Lerman S. (Ed.) Encyclopedia of Mathematics Education: Springer Reference href="www.springerreference.com Springer Verlag Berlin Heidelberg, 0. DOI: 10.1007/Springer Reference_313292.
Soto-Andrade, J. & Reyes-Santander, P. (2012). Mathematical Cognition in Juvenile Offenders: a Case Study, en Proceedings ICME 12 (July 2012, Seoul, Korea), pp. 4721-4730.
Steiner, R. (2009). Die zwölf Sinne des Menschen. 6ta Edición. Dornach: Rudolf Steiner.
Vigotsky, L. (1988). El desarrollo de los procesos psicológicos superiores. México: Editorial Crítica, Grupo editorial Grijalbo.
Vigotsky, L. (1995). Pensamiento y lenguaje. Buenos Aires: Ediciones Fausto.