INTRODUCCIÓN
La resolución de los problemas en la enseñanza de las Ciencias Naturales aparece en los programas de estudio como un objetivo de enseñanza. ¿Constituye la resolución de los problemas un contenido de la enseñanza de estas ciencias?
El contenido de la enseñanza lo integran “el sistema de conocimientos, el sistema de habilidades, la experiencia de la actividad creadora y el sistema de relaciones con el mundo” (Danilov, 1978, pág. 56).
Durante la resolución de los problemas los alumnos tienen que utilizar los conocimientos conceptuales (empíricos y teóricos) para poder explicar el cómo y el por qué de las contradicciones que están en los problemas al resolverlos. El saber no es suficiente para que un alumno resuelva el problema, él a menudo se realiza la siguiente pregunta ¿cómo lo hago?, demostrando qué tiene que saber hacer y para ello necesita utilizar los conocimientos procedimentales; la resolución de los problemas es uno de estos conocimientos que se enseñan en la escuela, pero el alumno también necesita emplear las habilidades generales y específicas de la ciencia durante la resolución del problema.
Entendiéndose por conocimiento procedimental, el conocimiento de los alumnos que le permite hacer algo, a partir de ejecutar un conjunto de acciones concretas que constituyen un modo de lograr el objetivo general, apoyados en los conocimientos conceptuales y las habilidades necesarias para ello.
Durante el proceso de resolución de los problemas con frecuencia el alumno se pregunta ¿cómo resolverlo? A la respuesta de esta pregunta se han dedicado muchos especialistas entre los que se encuentran psicólogos, matemáticos y físicos, elaborando distintos métodos generales de solución, independientemente de la variedad que existe, al resolver un problema hay que comprenderlo, ver cómo se va a resolver, resolverlo y ver si es correcta su solución.
En la actualidad al considerar la resolución de los problemas como objeto de enseñanza, una de las “tendencias es: La enseñanza de la resolución de problemas” (Rizo & Campistrous, 2002, pág. 12). El propósito de este artículo es explicar desde la teoría curricular el diseño del curso optativo para la enseñanza de la resolución de los problemas físicos-docentes, lo que posibilitó la elaboración del programa del curso.
DESARROLLO
A partir del grado de flexibilidad que se le otorga al currículo de la carrera de Licenciatura en Educación: Matemática – Física, el profesor elabora los cursos optativos que la carrera considera deben ser impartido. Al elaborar el programa un aspecto que no se puede soslayar es que el curso optativo debe responder al currículo de la misma. En el diseño del curso se “deben reflejarse las características de los modelos didácticos en que se sustenta y por tanto en ellos se refleja una estructura didáctica determinada” (Pino, Hernández, & Hernández, 2015, pág. 153), este es una obra humana que refleja una concepción que al ejecutarse pretende solucionar problemas y satisfacer necesidades, “el que se proyecta desde el pasado, se realiza en el presente, se deberá evaluar y modificar en el futuro, es un proceso que se está proyectando, ejecutando y evaluando en cada momento” (Addine, 2013, pág. 47), lo cual posibilita el perfeccionamiento de la formación del profesional de la educación.
El docente debe tener conciencia que él va a estar implicado en una actividad que se relaciona con una de las dimensiones del currículo, que es la de diseño curricular y que para ello debe tener presente las diferentes tareas de la misma que son:
1ra. Diagnóstico de problemas y necesidades.
2da. Modelación del Currículum.
3ra. Estructuración curricular.
4to. Organización para la puesta en práctica.
5ta. Diseño de la evaluación curricular (Paz, Miranda, Addine, & González, 2013, pág. 22).
Analicemos cómo se tuvieron en cuenta cada una de estas tareas durante el proceso de diseño durante el transcurso de la elaboración del programa del curso optativo. La primera tarea relacionada con el diagnóstico de problemas y necesidades concernidas con la resolución de problemas.
Se parte de analizar las causas que motivan las dificultades de los alumnos al resolver problemas, algunos autores plantean que están dadas porque no saben cómo actuar ante cada problema, unido a una falta de reflexión para enfrentarlo. Una importante argumentación que reafirma lo planteado al respecto considera que “por lo general los procedimientos metodológicos que se dan están dirigidos a acciones que debe realizar el maestro, es decir, es una metodología de enseñanza y no está dirigida a la búsqueda de procedimientos de actuación por el alumno” (Campistrous & Rizo, 1996, pág. X).
La falta de conocimiento en los alumnos de procedimientos para resolver un problema, provoca que dediquen poco tiempo a realizar la comprensión del texto del mismo, por lo que no pueden organizar su actividad y elaborar un plan para resolverlo, inclinándose exageradamente a la operacionalidad, “los alumnos comienzan a responder casi inmediatamente después de la primera lectura” (Pérez, 2012, pág. 158), se sostiene el criterio de que es necesario que en la escuela se realice la enseñanza – aprendizaje de los procedimientos que facilitan resolver los problemas
Existe una opinión mayoritaria entre algunos autores (Campistrous & Rizo, 1996); (Rizo & Campistrous, 2002); (Pino M. , 2005); (Pérez, González, & Sifredo, 2012); (Rebollar & Ferrer, 2014); (García O. , 2014); (Almeida & Almeida, 2016); (Guinjoan, Fortuny, & Gutiérrez, 2015); y, (Ramos, Castro, & Castro-Rodríguez, 2016), que al analizar las causas que inciden en las dificultades de los alumnos para resolver problemas, plantean que están dadas porque no saben cómo actuar ante cada problema, unido a una falta de reflexión para enfrentarlo. Ante esta situación resulta interesante reflexionar en la búsqueda de una solución, pues como se sabe, existe una relación importante entre la forma que se lleva a cabo el proceso de enseñanza-aprendizaje de la resolución de problemas en nuestras aulas y dicha problemática. En efecto, las dificultades detectadas requieren, dada su importancia, de una intervención didáctica adecuada en el marco de la enseñanza de la Física.
Modelación del curso optativo, en esta tarea debemos precisar las aspiraciones del curso en correspondencia con el modelo del profesional, al valorar los problemas profesionales que se deben atender, observamos que en uno de ellos se plantea “…la comprensión del rol y la importancia social de la física” (MINED, 2010, pág. 9), luego resulta necesario que se produzca un aprendizaje en los estudiantes donde “se combinen de forma dialéctica lo conceptual, lo experiencial y lo afectivo a partir del establecimiento de relaciones” (Perera, 2016, pág. 58), las que debe tener presente el profesor al proponerle a los estudiantes problemas físico-docentes que reflejen situaciones de la vida cotidiana, siendo necesario relacionar las habilidades y lo conocimientos físicos precedentes con los actuales.
Se plantea que al culminar los estudios los alumnos deben ser capaces de “Enseñar a formular y resolver problemas” (MINED, 2010, pág. 11). Luego este objetivo general deja bien precisado la necesidad de la enseñanza de la resolución de los problemas.
Dentro de las funciones del profesional que se forma está la función docente-metodológica, esta contiene las tareas dirigidas a que el educador en formación llegue a dominar las acciones esenciales de la docencia, entre las que se encuentra la enseñanza de la resolución de los problemas.
Una de las cualidades que debe tener el futuro profesor de Matemática y Física que se aspira formar es la “autoridad profesional expresada en el dominio de sus funciones y tareas profesionales con independencia y creatividad, así como de los contenidos de la Matemática y la Física” (MINED, 2010, pág. 14), el profesor debe dominar el método general de resolución de los problemas, así como los procedimientos que utiliza en el proceso de resolución.
Lo anteriormente planteado le permite cumplir con una de las tareas enunciada en la función docente metodológica que se refiera a “estructurar situaciones de aprendizaje” (MES, 2016, pág. 22), al considerarse como una de estas situaciones la resolución de los problemas físicos – docentes, el proceso de resolución de los problemas debe ser activo y el estudiante debe hallarle una significación vital a lo que aprende, un aspecto que los incentivar es: formular y resolver problemas vinculados a su entorno más cercano o a disímiles hechos y fenómenos de la realidad objetiva, que les permiten hacer valoraciones de carácter económico, político y social, particularmente en los que se demuestra la obra de la Revolución cubana (Álvarez, Almeida, & Villegas, 2014, pág. 35). Como representación del ideal que deben alcanzar los futuros profesores de Física, egresados del plan de estudio E, se refleja en los objetivos generales del modelo del profesional que durante su proceso formativo deben aprender a “elaborar y resolver tareas teóricas y experimentales” (MES, 2016, pág. 21), siendo la resolución de problemas una de esas tareas típicas que desarrolla un profesor de Física, en la literatura especializada esta es “vista como una actividad que produce en los estudiantes emociones positivas” (Mellado & et al, 2014, pág. 20), resulta necesario que esto sea atendido en los proyectos educativos de años para que se revelen las relaciones interdisciplinarias de la Física, aspectos a tener en cuenta durante la derivación de los objetivos de año. Dentro de los objetivos por año, se precisa desde el primero hasta tercer año la necesidad de resolver problemas de diferentes campos de la matemática y la física, que se resuelven con los recursos de las correspondientes asignaturas en el nivel medio, en tercero se plantea, enseñar a resolver problemas de las asignaturas Matemática y Física en la Secundaria Básica y en cuarto año se agrega la formulación de los problemas matemáticos y físicos. Luego los objetivos de años se han estructurado de forma tal que al culminar la carrera el estudiante sea capaz de resolver, enseñar y formular problemas, como lo plantea el objetivo general.
La estructuración curricular del curso optativo se efectúa una vez concluida la modelación, un momento importante es la ubicación del curso, esta se debe realizar en tercero o cuarto año, si se realiza en tercero se trabaja solo la enseñanza de la resolución de los problemas, si es en cuarto se trabaja también la formulación de los problemas, este curso se diseñó para cuarto año con una duración de 32 horas clases, en este momento ya los estudiantes comienzan a recibir Didáctica de la Física y de la Matemática.
La distribución temporal y por tipo de clase es la siguiente:
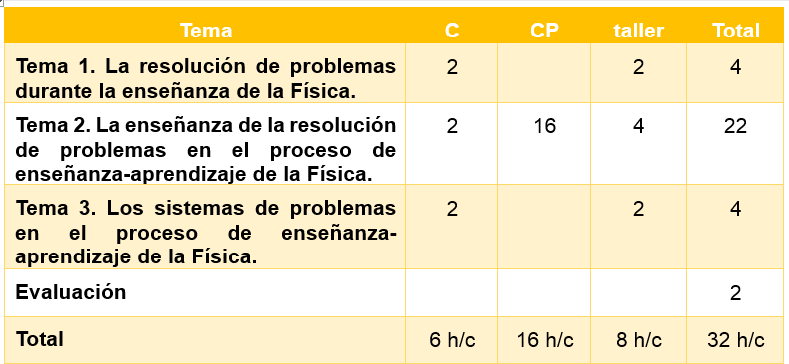
Tema 1. La resolución de problemas durante la enseñanza de la Física.
Objetivos del tema
- Definir problema físico-docente a partir que son problemas que se resuelven en el proceso de enseñanza-aprendizaje de la Física con los recursos de las correspondientes asignaturas en el nivel, sobre la base de la aplicación de procesos de pensamiento, procedimientos y estrategias de trabajo, el aprovechamiento de las tecnologías de la información y las comunicaciones.
- Identificar los tipos de problemas que se resuelven en el proceso de enseñanza-aprendizaje de la Física según la forma fundamental en que se presentan los datos.
- Identificar dificultades que presentan los estudiantes en la resolución de problemas durante el desarrollo del proceso de enseñanza-aprendizaje de la Físicautilizando métodos y formas habituales de la actividad científica como la búsqueda, procesamiento y comunicación de información en el lenguaje propio de la Didáctica de la Física.
- Argumentar el fundamento psicológico de la enseñanza de la resolución de los problemas físico-docentes en la escuela media cubana.
Sistema de conocimientos
La resolución de los problemas. Su importancia. Fundamentos psicológicos de la resolución de problemas. La resolución de los problemas y la enseñanza de la Física ¿Qué es un problema? Las condiciones y requerimientos de un problema. Los problemas físicos-docentes ¿Qué es un ejercicio? ¿Qué es la resolución de un problema? Agrupación de los problemas físico-docentes. Dificultades en la resolución de problemas en Física. Fundamentos psicológicos de la resolución de problemasTema 2. La enseñanza de la resolución de problemas en el proceso de enseñanza-aprendizaje de la Física.
Objetivos del tema
- Analizar diferentes tipos de modelos para la resolución de problemas que se pueden utilizar en el proceso de enseñanza-aprendizaje de la Física.
- Valorar el lugar que desempeña la comprensión de los problemas físico-docentes y la planificación de su resolución, durante la enseñanza de la resolución de problemas en la escuela media cubana.
- Resolver diferentes tipos de problemas según la forma fundamental en que se presentan los datos durante la enseñanza de la Física, sobre la base de la aplicación de procesos de pensamiento, procedimientos, estrategias de trabajo, el aprovechamiento de las tecnologías de la información y las comunicaciones.
- Enseñar a formular problemas relacionados con diferentes aspectos de la realidad económica, política y social, donde se manifiesten las relaciones ciencia-tecnología-sociedad-ambiente, utilizando contenidos de la física, sobre la base de la aplicación de procesos de pensamiento, que promuevan el desarrollo de la imaginación, de modos de la actividad mental, sentimientos, actitudes y valores acordes con los principios de nuestra sociedad.
Sistema de conocimientos
El método general de resolución de problemas. La comprensión de los problemas y la planificación de su resolución. La enseñanza de procedimientos (metodológicos y heurísticos) para la resolución de problemas. Niveles de ayuda que se pueden brindar a los estudiantes durante la enseñanza de la resolución de problemas. La formulación de problemas físico-docentes durante la enseñanza de la Física.
Tema 3. Los sistemas de problemas en el proceso de enseñanza-aprendizaje de la Física.
Objetivos del tema
Valorar la importancia de los sistemas de problema en el desarrollo del proceso de enseñanza aprendizaje de Física, a partir de las posibilidades que brindan para el tratamiento metodológico de una unidad y la planeación del sistema de clase, que promuevan el desarrollo de modos de actuación con un enfoque profesional pedagógico en su desempeño.
Sistema de conocimientos
Concepto de sistema. Los sistemas de problemas, su estructuración y lugar en el tratamiento metodológico de una unidad y la planeación de clase. Colección de problemas versus sistema de problemas.
La organización para la puesta en práctica del curso optativo desempeña un papel importante, en ella se debe prever las condiciones que dispone el profesor para el desarrollo del curso, este trabajo tiene en el centro al alumno para diagnosticar su desarrollo, sus avances, limitaciones, necesidades, intereses y sobre su base diseñar la organización del curso.
Un momento importante al diseñar el programa es la elaboración de las indicaciones metodológicas y de organización. Se trabajará con la idea de desarrollar el curso optativo lo más práctico posible, desarrollando un número alto de talleres, estas actividades permitirán una mayor participación en el debate de los temas, incentivando el interés de los participantes en la profundización del sistema de conocimientos que se aborden, permitiendo así alcanzar un intercambio fructífero que conlleve a un perfeccionamiento en su formación como docentes de Matemática y Física.
El tema uno se dedicará a estudiar los fundamentos psicológicos de la resolución de problemas, se debe trabajar en equipos, cada uno analiza una teoría y expone que la caracteriza, para en colectivo precisar por qué utilizamos el enfoque histórico cultural de Vigotsky como fundamento de la resolución de problemas. Se aprovecha la experiencia de los estudiantes en su práctica laboral para tratar lo que se entiende por problema y ejercicio, para después hablar de la necesidad de los problemas físicos-docentes, precisando los tipos de problemas, haciendo énfasis en su identificación por su presentación. Como parte del estudio independiente se selecciona un grupo de problemas, para que sean clasificados según la forma fundamental en que se presentan los datos.
A partir de la caracterización que ellos tienen de los grupos donde desarrollan su práctica laboral o de un instrumento que elaboren para investigar, se identifican las dificultades existen relacionadas con las habilidades que deben tener desarrolladas los estudiantes para resolver problemas en Matemática y Física.
En el tema dos, cuando se trabajen las tendencias didácticas en la resolución de problemas, se debe precisar que en el curso se enfatizará en la Enseñanza de la resolución de los problemas, se recomienda realizar un ejercicio metacognitvo con los estudiantes sobre ¿cómo enseña él a resolver problemas a sus alumnos? Cómo parte del estudio independiente los profesores deben investigar en sus grupos donde dan clases ¿qué etapas o pasos utilizan sus alumnos para resolver el problema? ¿Cuál es el método general que ellos utilizan en la resolución de un problema?
En este tema se debe dedicar atención a la enseñanza de los procedimientos para la resolución de los problemas que aparecen recogidos en la tarjeta de trabajo como medio que facilita su aprendizaje, se recomienda el empleo de hojas de trabajo en las clases para el aprendizaje de los procedimiento que facilitan comprender un problema, planificar cómo lo vamos a resolver y comprobar su solución, así como, su identificación de acuerdo a la forma fundamental en que se presentan los datos (Pino M. , 2005).
Si queremos enseñar a resolver problemas a los estudiantes es necesario la enseñanza y el aprendizaje de los procedimientos. Cada actividad de enseñanza que aspira a lograr un aprendizaje exitoso se tiene que desarrollar sobre la base de una concepción teórica segura. P. Ya Galperin, continuador de la obra de Vigotsky, aportó el desarrollo de la teoría de formación por etapas de las acciones mentales y los conceptos, mediante la cual establece los momentos funcionales y etapas de la actividad en el proceso de aprendizaje.
Hay que considerar que la asimilación los procedimientos para la resolución de los problemas, se tiene que estructurar como una relación dialéctica sujeta a cambios, entre la interiorización y la exteriorización, en la cual lo asimilado de forma consciente y activa se utiliza para la resolución de los problemas.
El primer encuentro de los estudiantes con el objeto del aprendizaje es de gran importancia, y en medida considerable determina el destino de la futura acción. En el proceso de asimilación es necesario garantizar al alumno los tres componentes funcionales en toda actividad: la parte orientadora (BOA), la ejecutora y la de control.
La base orientadora de la acción es “el sistema de condiciones en el que realmente se apoya el hombre al cumplir la acción esta debe tener un grado de integridad y generalidad que posibilite la asimilación de la acción” (Talízina, 1988, pág. 58).
Se asume una base orientadora de la acción (BOA) donde los orientadores estén representados en su forma generalizada, válido para todo tipo de problema.En este tipo de orientación los errores son insignificantes, produciéndose generalmente al comienzo de la enseñanza, además de que las acciones formadas poseen un buen nivel de estabilidad.
La orientación no se da aplicándola a un objeto concreto y por tanto la habilidad o acción que se está formando no se aplica únicamente para este objeto concreto, sino que permite que el individuo llegue a una orientación para cada caso particular, estimulando la actividad independiente del alumno y brindándole procedimientos de trabajo. Este tipo de BOA ofrece mayor posibilidad al protagonismo del alumno al resolver un problema físico - docente y aumenta las posibilidades de la creación.
La estructura que se recomienda en el proceso de formación de la acción mental tiene en cuenta las siguientes fases: orientación, formación de la acción mental y el control; y, aplicación.
Partiendo de esa estructura de la acción, Galperin considera que la fase de formación de la acción mental está compuesta por las siguientes etapas: “la acción en forma material materializada, la acción en forma de lenguaje externo; la acción en forma de lenguaje interno para sí y la acción en forma de lenguaje interno, mental” (Galperin, 1988, pág. 18).
Estas etapas explican los distintos momentos por los que transcurre el proceso de interiorización, a través del cual la acción que inicialmente se realiza en forma externa, se convierte en una acción mental.
Se sugiere además, dedicar tres clases a la formulación de problemas, comenzando por una primera etapa donde se modifican problemas ya resueltos anteriormente, para el desarrollo gradual de las habilidades creadoras de los estudiantes, se recomienda para ello: formular el problema dado realizando variaciones del contexto, de las condiciones y de las exigencias, donde la incógnita aparece como un dato y uno de los datos aparece como incógnita; escribir y resolver los problemas que tengan analogía con los ya resueltos; elaborar y resolver problemas, cambiando la situación de un problema ya resuelto y reformular y resolver el problema, introduciendo los cambios en la condición. (Filenko, 2008)
En la tercera clase los estudiantes elaboran problemas de forma independiente asumiendo como condición situaciones reales, relacionadas con los fenómenos y las leyes estudiadas, estos pueden tener las exigencias siguientes: reflejar situaciones creadas por los propios estudiantes; a partir de un experimento realizado y a partir de situaciones reales de la vida, relacionadas con los fenómenos y las leyes.
El tema tres se dedica a enseñar a los estudiantes la utilidad que tienen los sistemas de problema sobre las llamadas colecciones de problemas y ejercicios, a partir de las posibilidades que brindan para el tratamiento metodológico de una unidad y la planeación del sistema de clase, que promuevan el desarrollo de modos de actuación con un enfoque profesional pedagógico en su desempeño.
El diseño de la evaluación curricular.
La tarea de la evaluación curricular se enfrentó mediante una encuesta donde se valoran dos aspectos: lo que le aportó a su formación la asignatura optativa y el desarrollo del proceso de enseñanza – aprendizaje de esta asignatura, también se aplicó la técnica de lo positivo, lo negativo e interesante (PNI) al concluir el semestre.
Después de aplicados y procesados los instrumentos a los estudiantes se constatan los criterios siguientes: el curso optativo contribuyó a elevar sus conocimientos en la enseñanza de la resolución de problemas; era necesario porque es un problema del ejercicio de la profesión; el curso contribuye a la formación de un modo de actuación como futuro profesional de la educación y lo tratado en el curso impacta su formación docente metodológica.
Al valorar lo positivo, lo negativo y lo interesante del curso optativo se obtienen las siguientes opiniones, valoran como positivo: el conocimiento obtenido en el curso; el empleo de las hojas de trabajo; la preparación recibida en la enseñanza de la resolución de problemas para la escuela media; la contribución a su preparación para enseñar Física; la dinámica de las clases; la profundización de los contenidos de la escuela media y el hecho que le proporciona métodos y formas de trabajo.
Como negativo se expresa: poco tiempo para el desarrollo del curso y que no todos los estudiantes recibían la asignatura optativa.
Se considera interesante: la realización de problemas experimentales; la posibilidad de brindarles herramientas importantes para la enseñanza de la Física en la escuela media; el uso de la tarjeta de trabajo y la variedad de problemas presentados en las clases.
CONCLUSIONES
Al diseñar el programa de un curso optativo el profesor debe tener conciencia que él, va a estar implicado en la elaboración de un documento que expresa la concreción del currículo a un nivel micro, durante este proceso de elaboración las tareas del diseño curricular le sirven de guía durante la confección del documento.
El curso optativo diseñado e impartido durante el curso escolar 2014-2015, contribuyó a elevar el conocimiento de los profesores en formación sobre la enseñanza de la resolución de problemas, que constituye un problema profesional al que es necesario atender durante la carrera, el trabajo realizado mediante el empleo de la tarjeta y las hojas de trabajo contribuyen a formar un modo de actuación en los futuros egresados de la carrera de Matemática y Física.
REFERENCIAS BIBLIOGRÁFICAS
Addine, F. (2013). La Didáctica general y su enseñanza en la Educación Superior Pedagógica. La Habana: Pueblo y Educación.
Almeida, J., & Almeida, B. (2016). Capacitación del profesor que entrena para los concursos de Matemática en la Educación Media. Atenas Vol 3. Nro 35, julio-septiembre, pp. 47-63. Recuperado de: http://atenas.mes.edu.cu/index.php/atenas
Álvarez, M., Almeida, B., & Villegas, E. (2014). El proceso de enseñanza - aprendizaje de la Matemática. Documentos metodológicos. La Habana: Pueblo y Educación.
Campistrous, L., & Rizo, C. (1996). Aprender a resolver problemas aritméticos. La Habana. La Habana: Pueblo y Educación.
Danilov, M. (1978). Didáctica de la Escuela Media. La Habana: Pueblo y Educación.
Filenko, M. (2008). Competencia técnica para la elaboración de problemas físico-docentes. XX Encuentro Nacional sobre Enseñanza de la Física en el nivel Medio Superior, del 22 al 25 de septiembre 2008, Culiacán, Sinaloa.
Galperin, P. (1988). Desarrollo de las investigaciones sobre la formaciónes de acciones mentales. Conferencia. Centro de Estudio para el Perfeccionamiento de la Educación Superior. Universidad de la Habana.
García, O. (2014). Solución de problemas matemáticos de suma y resta en alumnos con dificultades para aprender. Atenas Vol 2. Nro 26, abril-junio, pp.38-53. Recuperado de: http://atenas.mes.edu.cu/index.php/atenas
Guinjoan, M., Fortuny, J. M., & Gutiérrez, A. (2015). Análisis del comportamiento de alumnos expertos resolutores de problemas en el contexto del concurso matemático Pruebas Cangur. Enseñanza de las Ciencias, 33. 1. Investigaciones didácticas. pp. 29-46. Recuperado de: http://dx.doi.org/10.5565/rev/ensciencias.1438
Mellado, V. & et al. (2014). Las emociones en la eseñanza de las ciencias. Enseñanza de las Ciencias, 32.(3). pp. 11-36. Recuperado de: http://dx.doi.org/10.5565/rev/ensciencias.1478
MES. (2016). Modelo del Profesional. Plan de Estudio "E". Carrera de Licenciatura en Educación. Física. La Habana, Cuba.
MINED. (2010). Modelo del profesional, plan D. Carrera de Licenciatura en Educación. Matemática - Física. La Habana, Cuba.
Paz, V., Miranda, T., Addine, F., & González, A. (2013). Currículo y contexto educativo. Habana: Pueblo y Educación.
Perera, A. (2016). La significatividad del aprendizaje de los contenidos químicos en la Licenciatura en Educación. Biología- Geografía. Tesis Doctor en Ciencias Pedagógicas. La Habana.
Pérez, N. (2012). La resolució de problemas:un estudio cualitativo de cómo los estudiantes lo hacen. En N. Pérez, E. Moltó, H. Rivero, C. Sifredo, & M. Lastra, Temas seleccionados de la Didáctica de la Física (pp. 152-160). La Habana: Pueblo y Educación.
Pérez, N., González, S., & Sifredo, C. (2012). La estimulación del pensamiento creador durante el aprendizaje e la Física: la resolución de problemas como actividad científica-investigativa. En N. Pérez, E. Molto, H. Rivero, C. Sifredo, & M. Lastra, Temas seleccionados de la Didáctica de la Física (pp. 125-151). La Habana: Pueblo y Educación.
Pino, M. (2005). Procedimientos metodológicos para la compresnión de los problemas físico-docentes y la planificación de su resolución en la escuela Secundari Básica. La Habana.: Tesis presentada en opción al grado científico de doctor en Ciencias Pedagógicas.
Pino, M., Hernández, A., & Hernández, M. (2015). Relación currículo didáctica: hilo conductor de la planeación diaria de la clase. Atenas.Vol 2 No 30 abril - junio, pp. 146-161. Recuperado de: http://atenas.mes.edu.cu/index.php/atenas
Ramos, L., Castro, E., & Castro-Rodríguez, E. (2016). Instrucción en el uso de esquemas para la resolución de problemas aditivos a estudiantes con necesidades educativas especiales. . Enseñanza de las Ciencias, 34.1. Investigaciones didácticas. pp. 173-192. Recuperado de: http://dx.doi.org/10.5565/rev/ensciencias.1765
Rebollar, A., & Ferrer, M. (2014). La enseñanza basada en problemas y ejercicios: una concepción didáctica para estimular la gestión aprendizaje del docente y del alumno. Atenas Vol 2. Nro 26, abril-junio, pp. 23-37. Recuperado de: http://atenas.mes.edu.cu/index.php/atenas
Rizo, C., & Campistrous, L. (2002). Didáctica de la resolución de problemas en Matemática. La Habana: IPLAC.
Talízina, N. (1988). Psicología de la enseñanza. Moscú: Progreso.