INTRODUCCIÓN
El fracaso en el aprendizaje de las matemáticas y en particular del cálculo en la universidad (Gibert, E. (2012); (González-Martín & Camacho, 2004), condujo a dos reflexiones importantes. La primera sobre la importancia de analizar y reconocer cómo los estudiantes construyen y justifican sus ideas en el estudio de los conceptos matemáticos y la segunda a la integración de un escenario didáctico experimental que involucre los recursos tecnológicos, el trabajo colaborativo, y el debate, para favorecer la argumentación en el estudio de la matemática (Okada & Simón, 1997), usando herramientas tecnológicas que permitan la transferencia entre diferentes sistemas de representación (Duval, 2000); (Hernández, Acevedo, Martínez & Cruz, 2014).
Las observaciones realizadas al trabajo de los estudiantes de ingeniería durante varios años (Arriaga, 2015), teniendo en cuenta las competencias que el sistema educativo mexicano exige para este nivel (ANUIES, 2013), motivó el desarrollo de la investigación. Al respecto, los trabajos de González-Martín (2005); García y Tintorer (2016) reportan dificultades, obstáculos y errores que presentan los alumnos universitarios al aprender los conceptos del cálculo diferencial e integral. Ellas son inherentes a los propios conceptos del análisis matemático, abordados en los niveles precedentes y otros se relacionan con la ausencia de significado de conceptos como límites, convergencia, definición de integral definida, series y sucesiones que se estudian en este nivel.
En la enseñanza de la matemática en ocasiones no se favorece la coordinación de los contextos de representación gráfico, algebraico y numérico, lo que eventualmente permitiría el tránsito y la transferencia de información entre estos contextos. Por años ha sido muy habitual la enseñanza de esta ciencia sobre la base de un fuerte trabajo algorítmico que conduce a la memorización de conceptos sin la posibilidad de problematizar su estructura y forma. En general el profesor se limita a exponer los conceptos, explicar procedimientos y resolver problemas, y el estudiante debe atender a la explicación y resolver ejercicios similares repitiendo los mismos pasos.
Así (Socas & Ruano, 2014), (Cuesta & Escalante, 2014), entre otros señalan que, en la resolución de ejercicios a estudiantes y profesores, se comprueba la existencia de dificultades para calcular sus valores y para realizar cálculos algebraicos, lo que induce a la valoración de que aplican un determinado algoritmo sin el análisis de las condiciones del problema y los casos particulares que en el estudio pueden aparecer.
Las herramientas y conceptos matemáticos tienden a ser enseñados desvinculados de los contenidos anteriores y descontextualizados; los estudiantes se limitan a memorizar un conjunto de criterios y técnicas que, de estar contextualizados, tendrían mucho más significado (García & Tintorer, 2016). Si bien, los estudiantes de los primeros años de la universidad poseen un manejo mecánico y operativo de muchos de los conceptos que deben utilizar en la disciplina matemática en la universidad (González-Martín & Camacho, 2004) se requiere reflexionar y reconocer el carácter variacional de ellos en las nuevas condiciones desde otras experiencias de trabajo y contextos de representación.
Las valoraciones realizadas permiten plantear que si se desarrolla una secuencia didáctica que favorezca el aprendizaje cooperativo, el debate científico y la autorreflexión conjugada con un ambiente tecnológico, se logra que los estudiantes universitarios de primer año expresen argumentos matemáticos, en los que es posible describir su construcción, contenido y estructura, así como la forma en que se realiza la transferencia de información entre las representaciones matemáticas, y los elementos conceptuales que tienen en cuenta para justificar sus hallazgos y establecer conexiones de ideas, entre otras.
En correspondencia con lo planteado el objetivo de la investigación fue desarrollar e implementar una secuencia didáctica de carácter experimental dirigida a estudiantes de primer año de universidad para el estudio de los argumentos matemáticos, que promueva representaciones espontáneas del tipo verbal y visual, y que favorezca la transición a las representaciones algebraica, gráfica y numérica en un ambiente tecnológico. Se puso especial atención en los argumentos que exponen los estudiantes durante la solución de la actividad en el contexto de trabajo colectivo, observando lo realizado en papel y computadora, así como el tránsito entre las representaciones, lo que permitirá identificar líneas de razonamiento que serán de utilidad para reorientar las actividades en clase y favorecer el aprendizaje. En la secuencia se usó el software de geometría dinámica GeoGebra, como medio para visualizar comportamientos, analizar la variación de las gráficas y agilizar procesos.
Desde el plano de la enseñanza este modelo de actividad matemática representó una novedosa experiencia de trabajo, ya que los estudiantes lograron apoyarse usando la tecnología [como un instrumento didáctico-cognitivo], con la intención de realizar sus propias experimentaciones y trabajar de forma colectiva en la solución de una actividad, en consonancia con lo expresado por la UNESCO (2013, 2014) La investigación condujo a reflexiones sobre el papel que tiene la herramienta tecnológica en la conformación de los argumentos matemáticos, particularmente en lo que se refiere al soporte de argumentos y a la estrecha relación de la visualización para sostener argumentos, matizar y exponer algunas excepciones de sus argumentos.
DESARROLLO
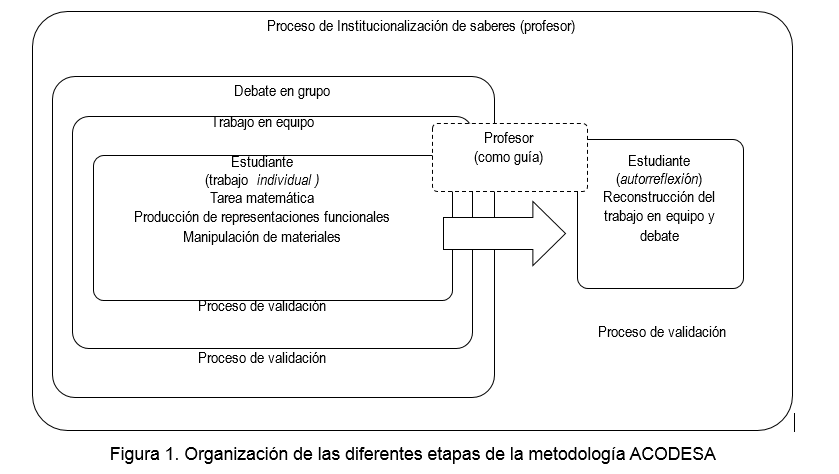
Para realizar esta investigación se integraron tres enfoques teóricos: ACODESA (Hitt, 2007), tránsito entre representaciones (Duval, 2000) y la argumentación (Inglis, Mejía-Ramos & Simpson, 2007), además se vinculan estos a un ambiente tecnológico (Mayorga, Navas & Pacheco, 2014); (Vacchieri, 2013). La secuencia didáctica se construyó empleando la metodología ACODESA (aprendizaje en colaboración, debate científico y autorreflexión) que proponen Hitt y González-Martín (2015). Esta metodología, se empleó para desarrollar la secuencia didáctica, considerando las oportunidades que brinda al coordinar el trabajo individual, trabajo en equipo y debate grupal. Además, este enfoque asume que el aprendizaje cooperativo, debate científico y autorreflexión son aspectos centrales del quehacer matemático en el aula, por lo que deben favorecerse y motivarse. Estas características conforman un escenario de trabajo escolar favorable para el estudio de los argumentos ya que los estudiantes tienen espacios para exponer y debatir sus ideas.
La metodología ACODESA contempla tres etapas; situación problema, problema y ejemplos-contraejemplos, con cinco fases cada una, que corresponden a tareas específicas y a formas de interacción: trabajo individual, en equipo, debate, autorreflexión e institucionalización de saberes. La primera etapa es denominada situación problema, donde se incluye un planteamiento introductorio contextualizado y situado a la actividad que en la matemática es esencial en el desarrollo de las ideas matemáticas (Rodríguez, 2015). En ella se motiva el pensamiento divergente, es decir, generar ideas creativas mediante la exploración de soluciones posibles de manera espontánea. Se favorece la reflexión sobre diferentes formas de interpretar la situación, se promueve la exploración y formulación de preguntas sobre posibles resultados de la actividad y puede conducir a un pensamiento convergente, caracterizado por dar respuesta con rapidez, precisión, centrado en el reconocimiento de regularidades y aplicación de técnicas, sin dar lugar a la ambigüedad. De acuerdo con Hitt (2007) una situación problema debe promover la apertura del pensamiento, que fomentará la aparición de representaciones funcionales.
La segunda etapa: problema, incorpora un planteamiento acotado que conduce a debates muy puntuales y respuestas específicas. Para Hitt (2007) esta etapa promueve también el pensamiento convergente-divergente y produce representaciones que vincula aspectos matemáticos, a través de la articulación entre representaciones y los procesos operatorios al interior de esas representaciones.
La tercera etapa: ejemplos-contraejemplos se caracteriza por un planteamiento práctico que sintetiza aspectos discutidos; se favorece el desarrollo de habilidades operatorias y de cálculo. Se coincide con Duval (2000) en que no sólo son importantes las tareas de transformación y conversión entre registros, sino también lo son la confrontación entre ejemplos y contraejemplos.
La cuarta etapa, se desarrolla en 5 fases que corresponden a diferentes tipos de actividad:
- trabajo individual, los estudiantes comienzan la construcción de representaciones funcionales para realizar determinada tarea y producir representaciones externas.
- trabajo en equipo, los estudiantes trabajan en las tareas separado (proceso de discusión y validación, refinamiento de las representaciones). El refinamiento de las representaciones externas se produce durante esta etapa por los debates al interior del equipo, donde cada uno aporta ideas para resolver la problemática.
- debate grupal, es un proceso de discusión y validación del refinamiento de las representaciones funcionales. Se dan a conocer los resultados y se analizan las relaciones que guardan las representaciones externas que les ayudaron a comunicar la situación del problema. El profesor promueve la exposición de ideas, estimula la participación e impulsa a establecer hipótesis, justificaciones y generalizaciones.
- autorreflexión (proceso de reconstrucción de tareas); se promueve una reflexión de lo realizado. El estudiante reconstruye, de forma individual la solución, justifica y valida sus conjeturas. En esta fase los estudiantes regresan individualmente a la tarea; es un proceso de reconstrucción de hechos y autorreflexión.
- proceso de institucionalización de saberes, el profesor inicia un proceso de integración y sistematización de saberes, utiliza las representaciones de los estudiantes y las complementa con las representaciones institucionales (gráfico, algebraico, numérico).
En la Figura 1 se ilustra la organización en la metodología ACODESA.
Douek (2007) define la argumentación como el acto de formar razones, hacer inducciones, sacar conclusiones y aplicarlas al caso en discusión, por tanto, es el proceso de producir un discurso lógicamente conectado sobre un tema, y un argumento como el producto de este proceso. Goizueta y Planas (2013) sintetizan que un argumento son las razones ofrecidas a favor o en contra de una proposición, mientras que una argumentación es el acto de producir razones. Al respecto, Inglis, Mejía-Ramos y Simpson, (2007) consideran al modelo de Toulmin (1958) como medio para analizar aspectos estructurales del proceso de argumentación en matemáticas.
El modelo de Toulmin (1958) (Figura 2) estudia los argumentos reconociendo la necesidad de analizar condiciones normativas de la argumentación en lenguaje natural, el que es aplicable a todas las argumentaciones y en particular a esquemas de prueba, tanto intuitivos y transformacionales como axiomáticos. El modelo está conformado por seis tipos de declaraciones que cumplen un papel diferente en el argumento. Ellos son: conclusión, dato, garantía, respaldo, calificativo modal, refutación. La conclusión es la tesis que defiende quien argumenta. El dato es la información en la que se basa la conclusión. La garantía justifica la conexión entre el dato y conclusión haciendo referencia, por ejemplo, a una regla, una definición, o a través de una analogía. La garantía es apoyada por el soporte a través de un nuevo dato.
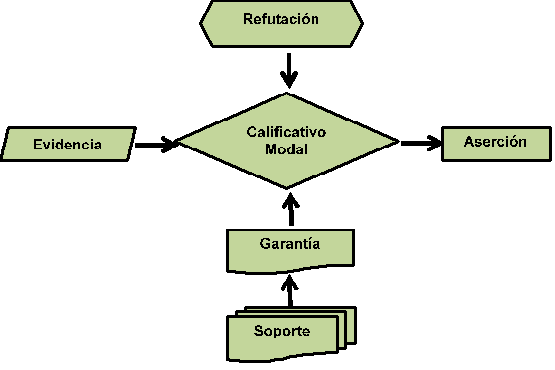
En su modelo, Toulmin acepta que una garantía acompañada de un calificativo modal no absoluto, puede ser propuesta para reducir el nivel de incertidumbre con respecto a una conclusión. El calificativo modal especifica la fuerza de la conclusión, expresa el grado de confianza de la tesis; la refutación presenta las excepciones de la conclusión, las condiciones bajo las cuales no es posible sostener la tesis del argumento.
El modelo de Toulmin opera así: a partir de un dato se formula una conclusión (proposición), una garantía conecta los datos con la conclusión y se ofrece un cimiento teórico, práctico o experimental: el respaldo. Los calificadores modales (grado de confianza): probablemente, seguramente, sin duda, tal vez, indican el modo en que se interprete la conclusión como verdadera, contingente o probable. En la refutación se considera sus posibles reservas u objeciones (limitaciones, excepciones, etc.).
En la investigación se incorporó al diseño didáctico, el ambiente tecnológico teniendo en cuenta que las herramientas tecnológicas permiten establecer nuevas tareas y configuran un ambiente de trabajo escolar experimental (Gutiérrez, 2015). La experimentación en un ambiente de uso de tecnología permite al estudiante construir conjeturas, transitar de un sistema de representación a otro, reconocer patrones, deducir y analizar comportamientos en gráficas y a partir de ello generar argumentos sobre un objeto matemático en construcción (Lalangui & Valarezo, 2017).
Se utilizó, en este caso, un software de geometría dinámica (GeoGebra) para involucrar a los estudiantes en un análisis visual de las gráficas y sus comportamientos, explorar formas, observar representaciones dinámicas, y establecer relaciones entre las diferentes representaciones, en un ambiente de trabajo experimental que favorece la manipulación de gráficas al variar parámetros y coeficientes.
En este contexto, la argumentación es importante, no sólo porque hace viable la observación de las ideas y nociones que el estudiante está concibiendo sobre un saber matemático, sino también, es una forma de generar o desarrollar ideas matemáticas sobre la base de sólidos conocimientos matemáticos (Gibert & Ballester, 2013).
Al respecto, Borges y Montes de Oca (2014) señalan que existen aspectos dinámicos de la matemática que se complementan con el uso de software para la producción de efectos visuales de los conceptos del cálculo, por lo que su uso en la enseñanza proporciona representaciones dinámicas de ellos y permite identificar las relaciones conceptuales, lo que favorece un ambiente de trabajo experimental donde se puedan realizar exploraciones a las gráficas. Baccaglini y Mariotti (2010) describen la actividad matemática denominada arrastre-conjetura en el contexto del estudio de la geometría dinámica que se refiere a la capacidad del software para realizar movimientos en tiempo real, que permite al usuario percibir el movimiento como el efecto de una acción (dependencia lógica), y conduce a identificar propiedades y regularidades. El análisis de los cambios observados ayuda a formular justificaciones matemáticas a través de la inducción y búsqueda de patrones.
Gibert y Ballester (2013) exponen que la construcción de un concepto matemático no se puede lograr si sólo se trabaja con un registro de representación, se deben promover tareas que favorezcan conversiones entre distintas representaciones, que permitan establecer la base cognitiva sobre la base de la contextualización a la realidad. Cada registro de representación resalta características y propiedades determinadas del objeto matemático, y su contenido depende más del registro de representación que del propio objeto, por tanto, es necesaria una interacción entre las diferentes representaciones para establecer un dominio conceptual más amplio.
Se coincide con Hitt (2007) en que las representaciones de un concepto matemático, solo son una parte del mismo, y que el tratamiento de las diferentes representaciones del concepto es lo que permitirá su construcción, es decir, son necesarias las tareas de conversión entre representaciones y la manipulación coherente de ellas. Establecer el tránsito entre representaciones requiere coordinar las experiencias de trabajo en las diferentes situaciones y planteamientos y transferir esta información a los diferentes contextos de representación. A partir de estos referentes, se construye la idea de transitar y articular basado en explorar conceptos, formular sus propias conjeturas, visualizar y extraer datos, aportar justificaciones, entre otros.
Sobre la base de lo anterior se elaboró una secuencia didáctica que permitiera confirmar o rechazar la hipótesis planteada. La secuencia didáctica sirve como escenario para analizar los argumentos expuestos por los estudiantes durante la resolución de las actividades matemáticas. La actividad del estudiante, en un contexto de experimentación y un trabajo coordinado entre papel, lápiz y tecnología, se orienta a favorecer el tránsito entre representaciones (algebraica, numérica y gráfica).
Se utilizó el modelo de Toulmin como un instrumento de recolección y análisis de datos del contenido y estructura de los argumentos expuestos por los estudiantes.
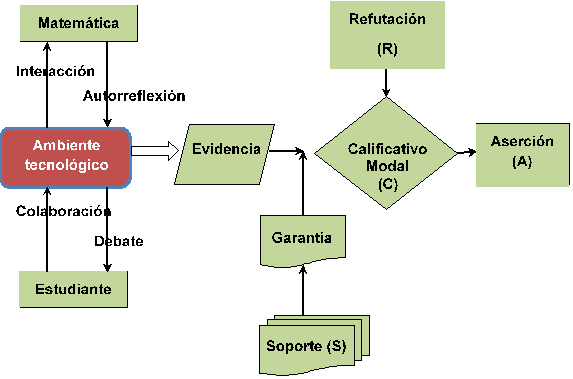
En la Figura 3 se presenta el esquema que describe el modelo en el que se ubica el ambiente tecnológico como mediador en la construcción de argumentos matemáticos, el que se obtiene en esta investigación.
La secuencia didáctica se implementó en el Instituto Tecnológico Superior de Tantoyuca, Veracruz-México, participaron 24 estudiantes del segundo semestre de la carrera de Ingeniería Industrial. De acuerdo con la metodología ACODESA (Hitt & González-Martín, 2015) se formularon tres etapas, en las dos primeras se establecieron 5 fases de forma secuencial y con tiempos predeterminados (trabajo individual, trabajo en equipo, debate, autorreflexión, proceso de institucionalización), en el desarrollo de la tercera etapa no se consideraron tiempos predeterminados.
Etapa 1: situación problema contextual. Para la puesta en práctica de la secuencia didáctica se utilizaron situaciones problema de la industria petroquímica.
Intención matemática del problema: Elaborar dibujos a escala, con el propósito de representar la situación problema, considerando las especificaciones dadas y aplicar teoremas o métodos. Recuperar conocimientos previos para al aplicarlos obtener el modelo matemático (función) que representa la situación problema y aplicar teoremas usando las condiciones solicitadas por el teorema. Compartir resultados obtenidos a lápiz y papel y dar cuenta de las ventajas y desventajas de usar los teoremas y construir una maqueta a escala considerando los datos obtenidos en los incisos anteriores.
Intención didáctica. Deben formular una primera aproximación de la representación gráfica del modelo matemático de la situación con: papel, reglas, compás, juego de escuadras, plumones, calculadora, etc. Apoyados del GeoGebra, harán comparaciones entre las representaciones para contrastar características y discutir diferencias. Formularán predicciones sobre el comportamiento de la función desde la gráfica.
Etapa 2: utilización de nuevos problemas. Se plantearon 10 problemas contextuales (Ingeniería Industrial), relacionados con otras asignaturas del mismo semestre.
Intención matemática. Acercamiento a conocimientos previos: función, utilización de propiedades, generalización de teoremas y visualización de los efectos de las variaciones encontradas. Comparación de los resultados obtenidos al usar las condiciones dadas contra los valores de las tablas realizadas
Intención didáctica. Se enfrentan a problemas que conducen a debates muy puntuales y respuestas específicas, presentan conjeturas y justificaciones a través de la articulación entre representaciones basado en un trabajo equilibrado entre papel, lápiz y tecnología.
Etapa 3: utilización de ejemplos-contraejemplos que conducen a generalizaciones de lo estudiado hasta el momento.
Intención matemática. En el ejercicio 1 (ejemplo con varios incisos del mismo tipo) se solicitó justificar cada uno. Los estudiantes usaron el GeoGebra con la función deslizador, como control de forma remota, pero dentro del área de trabajo, que permite mover o deslizar un punto sobre una figura, visualizándose una animación.
En el ejercicio 2 (contraejemplos), con 6 contraejemplos que se solicitan justificaciones, esto con la intención que los estudiantes apliquen las propiedades. Se pide analizar las características de las funciones para aplicar la propiedad que corresponda. Para realizar estas actividades se necesita transitar entre representaciones (gráfica, numérica y algebraica) con la intención de encontrar datos que justifiquen los resultados.
Intención matemática. Usar lar propiedades adecuadas para cada caso.
Intención didáctica. Deben confrontar ejemplos y contraejemplos relacionados con el concepto en estudio para justificar el resultado, trabajan en diferentes registros de representación y articulan las tareas papel, lápiz y tecnología. En cada caso exploran, y experimentan usando la función deslizador del GeoGebra para justificar los resultados.
Para la valoración de los resultados obtenidos se recolectaron primeramente los datos. Como instrumento para la recolección y el análisis de los datos se empleó el modelo de Toulmin con el propósito de describir la construcción, contenido y estructura de los argumentos al transitar entre diferentes representaciones durante el desarrollo de sus actividades a papel-lápiz y tecnología.
De los 24 estudiantes, se eligieron cuatro que mostraron disposición y voluntad de participar en la etapa de entrevista semiestructurada; ellos se organizaron en dos equipos (mujer y hombre), el entrevistador (investigador) tuvo la función de coordinar la entrevista. En la entrevista se les presentó una consigna para ser resuelta de forma colaborativa durante 60 minutos previos al diálogo. La entrevista se estructuró con cuestionamientos flexibles alrededor de un ejercicio no rutinario (contraejemplo). Su intención fue que verbalizaran sus ideas respecto a los elementos del modelo e identificar las características de los argumentos expuestos al realizar sus tareas en un ambiente tecnológico. Se prestó especial atención en el uso del calificativo modal y la refutación para investigar la fortaleza de los argumentos expuestos.
Los resultados condujeron a reflexiones sobre el papel que tiene el ambiente tecnológico en un trabajo articulado: individual, colaborativo, debate y autorreflexión, en la conformación de los argumentos matemáticos, particularmente en lo que se refiere al soporte de argumentos; por ejemplo, la pareja 2 construyó un esquema argumentativo muy fundamentado y la pareja 1 no lo logró adecuadamente. Es importante matizar, la estrecha relación de la visualización para sostener argumentos y exponer algunas excepciones de sus argumentos. Al variar parámetros usando la función deslizador, fue necesario analizar el comportamiento (visualizar) para extraer datos y desarrollar ideas.
La actividad matemática denominada arrastre-conjetura en un contexto de uso de tecnología, describe procesos cognitivos que ocurren en la producción de conjeturas (Baccaglini & Mariotti, 2010). En ella se desarrollan ideas en la fase de exploración que evolucionan hasta la formulación de conjeturas. Al usar la función deslizador, los estudiantes construyeron la tabla de convergencia que propició el tránsito y articulación entre representaciones que permitió obtener los datos y exponer analogías para las justificaciones. El análisis de los cambios observados ayudó a los estudiantes a formular justificaciones matemáticas a través de la inducción y búsqueda de patrones.
Por tanto, se puede afirmar que la actividad matemática en un ambiente de trabajo individual, colaborativo, de debate, y autorreflexión favorece un contexto de trabajo matemático en el que los estudiantes exponen sus ideas y razonamientos y desafían las afirmaciones de los demás integrantes para lograr el objetivo de búsqueda de consensos. Los estudiantes y el profesor podrían iniciar un debate en el aula en la que las conjeturas y justificaciones encontradas podrían llegar a ser demostraciones formales. Este modelo de trabajo, se fortalece cuando los estudiantes realizan una transferencia de información entre las representaciones matemáticas, ya que se ven motivados a justificar sus hallazgos y establecer conexiones de ideas.
Se coincide con la señalado en Álvarez, Hernández, Cabreras y Herrero (2013) en que este tipo de diseños en ambientes tecnológico dinámicos, permite a los estudiantes explorar los conceptos, formular sus propias conjeturas, probar las conjeturas y discutirlas en un ambiente de clase general. Este modelo de trabajo se fortalece cuando los estudiantes realizan una transferencia de información entre las representaciones matemáticas, ya que se ven motivados a justificar sus hallazgos y establecer conexiones de ideas. El acto de dar una explicación o argumentación para una solución no es un comportamiento habitual entre los alumnos, sino que debe ser construido como parte del contrato didáctico en el aula de matemáticas.
CONCLUSIONES
Se logra articular el modelo Toulmin en el proceso de enseñanza-aprendizaje de la matemática, con la metodología ACODESA, realizando aportaciones a esta, al incorporar a los momentos específicos para el trabajo individual, en equipo y debate grupal, en un enfoque que asume el aprendizaje cooperativo, el debate científico y la autorreflexión, el uso del ambiente tecnológico, y la utilización de contraejemplos, conjeturas y problemas abiertos, logrando una conjugación perfecta en la determinación de argumentos matemáticos con la utilización de conceptos matemáticos.
La elección del software de geometría dinámica (Geogebra) que se caracteriza por tener elementos como el deslizador, permite a los usuarios interactuar dinámicamente y observar cómo otros elementos responden a las condiciones alteradas, lo que en el modelo de actividad matemática denominada arrastre-conjetura describe procesos cognitivos que ocurren durante la producción de conjeturas.
El ambiente de trabajo colaborativo, se fortalece cuando se realizan transferencias de información entre las representaciones matemáticas [gráfica, numérica y algebraica] mediante un trabajo equilibrado y articulado papel-lápiz-tecnología, al verse motivados a justificar sus hallazgos y establecer conexiones de ideas.
REFERENCIAS BIBLIOGRÁFICAS
Álvarez, A., Hernández, L., Cabreras, J. F. & Herrero, E. (2013). Estudio de las dimensiones de la integración de las TIC en una universidad tecnológica cubana. Revista Cubana de Ingeniería. Vol. IV, No. 3, pp. 5 -14.
ANUIES (2013). Estatuto de la Asociación Nacional de Universidades e Instituciones de Educación Superior de la República Mexicana, A.C. México: ANUIES.
Arriaga, M. (2015). El diagnóstico educativo, una importante herramienta para elevar la calidad de la educación en manos de los docentes. Atenas. Vol.4. No. 31, pp. 63-75. Recuperado de: http://atenas.mes.edu.cu
Baccaglini, A. & Mariotti, M. A. (2010). Generating Conjectures in Dynamic Geometry: the Maintaining Dragging Mode. International Journal of Computers for Mathematical Learning, Vol.15, No.3, pp. 225-253.
Borges, J. T. & Montes de Oca, L. (2014). Las formas de trabajo y de pensamiento de la matemática en los recursos de un software educativo. Atenas. Vol. 2 No. 26, pp.91-100. Recuperado de: http://atenas.mes.edu.cu
Cuesta, A. & Escalante. J. E. (2014). Competencias algebraicas: ¿qué dominan los estudiantes universitarios. Atenas Vol. 2 No. 26, pp. 9-22. Recuperado de: http://atenas.mes.edu.cu
Douek, N. (2007). Some remarks about argumentation and proof. In BOERO, P. (Ed.) Theorems in School: From history, epistemology and cognition to classroom practice. Rotterdam: Sense Publishers, pp. 163-181.
Duval, R. (2000). Basic Issues for Research in Mathematics Education, In 24th Conference of the International Group for the Psychology of Mathematics Education (PME24), Hiroshima. Japón, pp. 55-69.
García, H. & Tintorer, O. (2016). Organización de la actividad de situaciones problema en Matemática. Atenas. Vol. 3. No.35. pp. 31 – 46. Recuperado de: http://atenas.mes.edu.cu
Gibert, E. (2012). Una alternativa didáctica para la estructuración del proceso de enseñanza-aprendizaje en las clases de la asignatura Matemática en la Educación Secundaria Básica. Tesis en opción al Grado de Doctor en Ciencias Pedagógicas, Universidad de Ciencias Pedagógicas “Enrique José Varona”, La Habana.
Gibert, E. & Ballester, S. (2013). Promoviendo el aprender a aprender matemática en las clases de la educación secundaria básica. Atenas. Vol 4. No. 21, pp. 103-118. Recuperado de: http://atenas.mes.edu.cu
Goizueta, M. & Planas, N. (2013). Temas emergentes del análisis de interpretaciones del profesorado sobre la argumentación en clase de matemáticas. Enseñanza de las Ciencias, Vol. 31, No.1, pp. 61-78.
González-Martín, A. S. (2005). Use of examples and counterexamples in University teaching: The Improper Integral. In North American Chapter of the International Group for the Psychology of Mathematics Education, Virginia, Virginia, USA, pp. 1-7
González-Martín, A. S. & Camacho, M. (2004). What is firts-year mathematics students’ actual understanding about improper integration? International Journal of Mathematical Education in Science and Technology, Vol. 35, No.1, pp. 73-89.
Gutiérrez, Y. S. (2015). Prácticas pedagógicas y apropiación de las TIC en los docentes del colegio Nuevo Reino de Granada. Universidad de Manizales. Colombia.
Hernández, L., Acevedo, J., Martínez, C. & Cruz, B. (2014). El uso de las TIC en el aula: un análisis en términos de efectividad y eficacia. Congreso Iberoamericano de Ciencia, Tecnología, Innovación y Educación. Buenos Aires.
Hitt, F. (2007). Utilisation de calculatrices symboliques dans le cadre d´une méthode d´apprentissage collaboratif, de débat scientifique et d´auto-réflexion. In Baron, M.; Guin, D.; Trouche, L. (Eds.) Environnements informatisés et ressources numériques pour l´apprentissage: conception et usages, regards croisés, Col. Systémes de formation et d´enseignement, pp. 1-25.
Hitt, F. & González-Martín, A. S. (2015). Covariation between variables in a modelling process: The ACODESA (collaborative learning, scientific debate and self-reflection) method. Educational Studies in Mathematics, Vol. 88, No. 2, pp. 201–219.
Inglis, M., Mejía-Ramos, J. & Simpson, A. (2007). Modelling mathematical argumentation: The importance of qualification. Educational Studies in Mathematics, Vol.66, No.1, pp. 3-21
Lalangui, J. & Valarezo, J. (2017). El aprendizaje, la era del conocimiento y las TIC ante la realidad Universitaria Ecuatoriana. Atenas. Vol 2. No. 38, pp. 51 – 65. Recuperado de: http://atenas.mes.edu.cu
Mayorga, A., Navas, Y. & Pacheco, S. (2014). Desafíos pedagógicos ante el uso de las tecnologías de la información. YACHANA, Revista Científica, 3(2), pp. 126-137.
Okada, T. & Simon, H. A. (1997). Collaborative discovery in a scientific domain. Cognitive Science, Vol. 21, No. 2, pp. 109-146.
Rodríguez, L. (2015). El método de proyecto para la formulación de problemas matemáticos. Atenas. Vol. 4. No. 32, pp. 100-113. Recuperado de:http://atenas.mes.edu.cu
Socas, M. & Ruano, R. (2014). La competencia matemática formal. Aplicaciones al análisis del contenido y al desarrollo curricular en matemáticas. Atenas. Vol. 2 No. 26, pp. 1-8. Recuperado de: http://atenas.mes.edu.cu
Toulmin, S. (1958). The uses of argument. New York: Cambridge University Press.
UNESCO (Organización de las Naciones Unidas para la Educación, la Ciencia y la Cultura). (2014). Políticas TIC en los sistemas educativos de América Latina. Francia.
UNESCO. (2013). Enfoques estratégicos sobre las Tics en Educación en América Latina y El Caribe. Chile.
Vacchieri, A. (2013). Estado del arte sobre la gestión de las políticas de integración de computadoras y dispositivos móviles en los sistemas educativos. Editorial Argentina.